一、瀑布图
1. 什么是瀑布图?
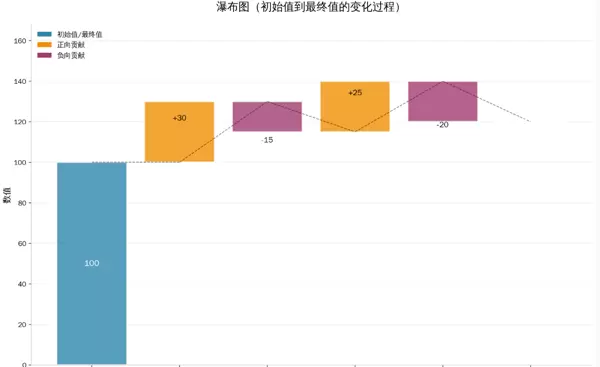
瀑布图亦称桥接图或阶梯图,是一种独特数据可视化形式,通过连续的柱形条展示初始值经由一系列正负贡献因素最终达到终结值的过程。例如,下图即为典型的2D瀑布图。
初始值设为100,经历4个正负贡献因素(产品A增长+30、产品B下滑-15、市场扩张+25、成本增加-20)后,最终达到120。蓝色柱代表初始值和最终值,橙色柱表示正向贡献,紫色柱表示负向贡献。虚线连接各阶段数值,直观地展示了数值的连续变化过程。
2. 瀑布图的背景与优势
瀑布图源自财务管理领域,最初应用于财务分析,自20世纪90年代起在企业财务报告中广泛采用,其名称来源于图表形态类似瀑布的阶梯式变化。此图表以首根柱形条表示起始值,中间柱形条展示各项增减变化(正值表示增长、负值表示减少),最后一根柱形条呈现最终值,并通过色彩区分正负影响。瀑布图的主要优点在于能直观展示数据构成关系,清晰呈现从起点到终点的全过程及其各因素的贡献度;它能迅速识别关键驱动因素,明确显示正面与负面贡献者;通过将复杂数值关系可视化,有效减轻认知负担,便于向非技术人士解释数据;同时为根本原因分析和决策提供强有力的支持,帮助组织发现改进机会并进行情景比较。随着数据可视化工具的进步,瀑布图已从财务领域逐渐扩展至业务分析、项目管理等多个应用场景。
3. 瀑布图的适用场景
瀑布图具备广泛的应用场景,在财务分析这一传统应用领域中,它常用于利润分析中展示从收入到净利润的全过程、现金流分析中呈现期初至期末现金的变化、预算与实际差异的解析以及成本构成的逐项展示;在业务绩效分析方面,瀑布图能有效分析销售业绩的目标与实际差异、客户数量变化因素、库存水平驱动因素以及市场份额变化的贡献分析;在项目管理和运营中,它适用于项目成本的预算与实际差异分析、项目进度的时间消耗分析、资源使用的构成分析以及KPI达成情况的因素分析;在数据分析和报告领域,瀑布图还可用于数据汇总的交叉验证、变化趋势的驱动因素分析、不同时间段或版本的对比研究以及问题原因的逐层分解,展现了强大的多场景适用性。
瀑布图之所以受到欢迎,是因为它能够将单调的数字表格转换为具有故事性的视觉叙述,使数据分析更加生动且易于理解。接下来我们将展示3D瀑布图,更生动形象地展现瀑布图的魅力。
4. 代码实现3D瀑布图
1. 代码
import matplotlib
matplotlib.use('TkAgg') # 使用 TkAgg 后端
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
import numpy as np
def line_3d(x, y, z, x_label_indexs):
"""
在y轴的每个点,向x轴的方向延伸出一个折线面:展示每个变量的时序变化。
x: x轴,时间维,右边。
y: y轴,变量维,左边。
z: z轴,数值维。二维矩阵,y列x行。每一行是对应变量的一个时间序列。
x_label_indexs: 需要标注的时间点。
"""
x_num = len(x)
y_num = len(y)
if z.shape[0] != y_num or z.shape[1] != x_num:
print(f"形状不匹配: z.shape={z.shape}, y_num={y_num}, x_num={x_num}")
return -1
# 制作坐标格点
X, Y = np.meshgrid(x, y)
# 创建画布和3D坐标轴
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
# 绘制折线面
for i in range(y_num):
# 数据线
ax.plot(X[i], Y[i], z[i], color=plt.cm.viridis(i / y_num),
linestyle='-', linewidth=2, marker='o', markersize=4)
# 基线(z=0)
ax.plot(X[i], Y[i], np.zeros_like(z[i]), color='gray', alpha=0.5, linewidth=1)
# 创建填充多边形
verts = []
for j in range(x_num):
verts.append([X[i, j], Y[i, j], z[i, j]])
for j in range(x_num - 1, -1, -1):
verts.append([X[i, j], Y[i, j], 0])
poly = Poly3DCollection([verts], alpha=0.3)
poly.set_color(plt.cm.viridis(i / y_num))
ax.add_collection3d(poly)
# 标注数值
for k in x_label_indexs:
if k < x_num: # 确保索引有效
ax.text(X[i, k], Y[i, k], z[i, k] + 0.05, f'{z[i, k]:.2f}',
color='black', ha='center', fontsize=8)
# 连接标注点
for k in x_label_indexs:
if k < x_num: # 确保索引有效
ax.plot(X[:, k], Y[:, k], z[:, k], '--', color='gray', alpha=0.7)
# 设置标签
ax.set_xlabel('Time')
ax.set_ylabel('Variables')
ax.set_zlabel('Values')
ax.grid(True)
plt.tight_layout()
plt.show()
if __name__ == '__main__':
time = np.arange(1, 15, 2) # x轴:时间
x = np.arange(5) # y轴:变量
z = np.array([
[0.20, 0.34, 0.38, 0.43, 0.44, 0.50, 0.61],
[0.21, 0.40, 0.38, 0.43, 0.60, 0.72, 0.75],
[0.22, 0.43, 0.44, 0.60, 0.77, 0.84, 0.92],
[0.23, 0.42, 0.44, 0.43, 0.64, 0.77, 0.86],
[0.38, 0.42, 0.43, 0.49, 0.55, 0.60, 0.81]
])
line_3d(time, x, z, [1, 4, 6])时间轴
准备了7个等间距的时间点(1, 3, 5, 7, 9, 11, 13),代表观察的时间序列。
变量轴
定义了5个需分析的变量,用数字0到4表示。
数值矩阵
是一个5行7列的二维数组,每行对应一个变量在7个时间点上的测量值,每列对应同一时间点下5个变量的数值。从数据中可以看出,所有变量均呈现总体上升趋势,但增长速率和模式各有不同——有些稳定增长,有些有波动,有些起点高但增长缓慢,有些起点低但增长迅速。
标注点
指定了需特别关注的3个时间点(索引1、4、6,对应实际时间点3、9、13),这些点将在可视化中被突出显示。
2. 结果展示
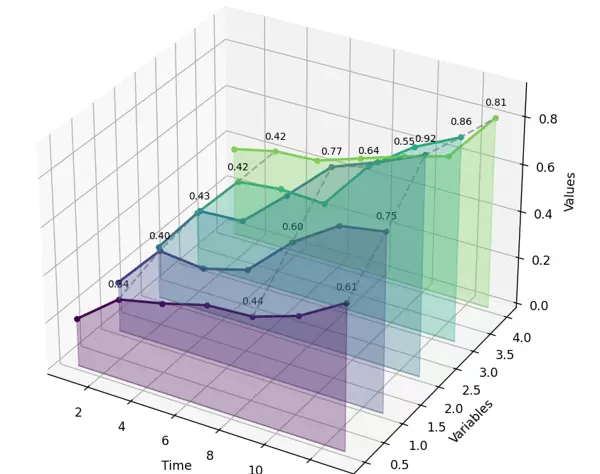
增长趋势:
所有5个变量均呈上升趋势
增长速率和模式各不相同
最高值达0.92,最低起始值0.20
变量对比:
变量2(绿色)增长最为显著:0.22 → 0.92
变量4(紫色)起点最高但增长缓慢
变量0(蓝色)增长最慢
时间节点:
在时间点3、9、13有重点标注
虚线连接显示同一时间点的横向对比
由于是3D瀑布图,因此该图可以任意拖动旋转。
5. 与传统图表对比
| 图表类型 | 优势 | 劣势 |
|---|---|---|
| 3D瀑布图 | 多维数据、趋势直观、空间利用高效 | 不适用于数据点过多的测试 |
| 多折线图 | 数值精确、制作简单 | 线条交叉混乱、对比困难 |
| 堆叠面积图 | 总量清晰、构成明确 | 个体趋势不明显 |
3D瀑布图通过三维展示解决了多变量时间序列数据的可视化挑战,它使得数据的时间趋势、变量对比、数值关系三个维度同时可见,尤其适合需要综合分析多个指标变化规律的场景。尽管制作比传统图表复杂,但在数据洞察深度上具有明显优势。
二、山峦图
在数据可视化中,有一类图表宛如层叠的山峦,能直观展现数据分布随类别(如时间、组别)的变化趋势,这就是山峦图(Mountain Plot),也常被称为堆叠密度图或脊线图的一种变体。今天和大家分享山峦图的原理以及如何使用Python实现它。
1. 什么是山峦图?它有何用途?
假设你有12个月的用户消费数据分布,希望同时对比每个月的消费金额“集中趋势”和“波动情况”,使用普通的直方图或密度图会显得拥挤,而山峦图则能将每个类别的数据分布“叠放”成连绵的“山脉”,既保留了单组数据的分布特征,又能直观对比组间差异。
其核心价值在于:
多组分布对比:清晰展示不同类别(如时间、群体)下数据分布的形状、峰值、离散程度。
趋势感知:通过“山脉”的高低、宽窄变化,快速捕捉数据随类别变化的趋势。
视觉层次感
堆叠的方式避免了图表的拥挤,使得复杂的多组分布对比更加直观。
山峦图的设计原理与关键元素
以 “月份 - 数据分布” 的情境为例,剖析山峦图的设计逻辑:
- 数据分布的 “高度”—— 核密度估计(或直方图)
对于每个类别(如 “Jan”),需先描绘其数据的分布形态。可用核密度估计(KDE)或直方图来完成:
- 核密度估计:通过平滑的线条描绘数据的概率密度分布,展现出“山峦”的流畅感。
- 直方图:采用矩形块堆砌显示分布,风格更为硬朗(本文以核密度为例)。
- 类别的 “堆叠”—— 垂直方向的位置调整
为了确保不同类别的 “山脉” 不相互重叠,需为每个类别设定一个垂直基准点,然后将其分布曲线 “堆叠” 在该基准之上。例如,12 个月可按顺序分配垂直坐标,使 “Jan” 位于底部,“Dec” 处于顶部。
- 视觉编码 —— 色彩与透明度
利用连续的色彩映射(如
色阶)来区分不同的类别,同时适当调节透明度,使 “山脉” 的层次更加柔和,减少视觉遮挡。Spectral
用 Python 绘制山峦图
以下是结合代码解析如何实现山峦图:
- 数据准备
模拟了12 个月的正态分布数据,每个月的分布平均值呈现 “先增后减” 的趋势,以此展现山峦图的对比效果。
import matplotlib.pyplot as plt import numpy as np # 模拟数据:为12个月生成不同均值的正态分布数据 def generate_normal_data(mean, std=1.2, size=1000): np.random.seed(6) # 固定随机数种子,保证结果可复现 return np.random.normal(mean, std, size) months = ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec'] data_dict = {} # 前6个月均值递增,后6个月均值递减 for i in range(6): data_dict[months[i]] = generate_normal_data(i * 2) / 10 for i in range(6, 12): data_dict[months[i]] = generate_normal_data((11 - i) * 2) / 10 - 核心绘图函数 —— 构建 “山峦” 的形状
将绘图逻辑封装在
函数中,主要步骤包括颜色映射、核密度估计、堆叠绘制:mountain_plotdef get_colors_from_map(color_num, cmap_name="Spectral"): """从matplotlib色阶中获取连续颜色""" cmap = plt.get_cmap(cmap_name) return cmap(np.linspace(0, 1, color_num)) def mountain_plot(data_dict, colors=None): if colors is None: # 自动生成与类别数量匹配的连续色阶 colors = get_colors_from_map(len(data_dict), "Spectral") # 提取类别(如月份)和垂直位置 categories = list(data_dict.keys()) y_positions = [2 * i for i in range(len(categories))] # 每个类别垂直方向的基准位置 # 创建画布 fig, ax = plt.subplots(figsize=(8, 12)) # 逐个类别绘制“山峦” for i, cat in enumerate(categories): data = data_dict[cat] # 核密度估计:先通过直方图得到密度分布,再转换为bin中心 density, bins = np.histogram(data, bins=30, density=True) bins = 0.5 * (bins[1:] + bins[:-1]) # 转换为bin的中心,让曲线更平滑 # 绘制填充区域(山峦的“山体”) ax.fill_between( bins, y_positions[i] + density, # 上边界:基准位置 + 密度高度 y_positions[i], # 下边界:基准位置 facecolor=colors[i], alpha=0.7 # 透明度,增强层次感 ) # 绘制密度曲线(山峦的“轮廓”) ax.plot(bins, y_positions[i] + density, color=colors[i], linewidth=1.5) # 配置Y轴:用类别名称作为标签 ax.set_yticks(y_positions) ax.set_yticklabels(categories) # 优化视觉效果:网格线与边框 ax.grid(axis='y', linewidth=1, color='gray', alpha=0.2) # 仅显示Y轴方向的网格 ax.spines['top'].set_visible(False) ax.spines['bottom'].set_visible(False) ax.spines['right'].set_visible(False) ax.spines['left'].set_visible(False) plt.tight_layout() # 自动调整布局,避免标签重叠 plt.show() - 运行绘图
调用函数即可生成山峦图:
if __name__ == '__main__': mountain_plot(data_dict)
完整代码展示
import matplotlib.pyplot as plt
import numpy as np
def get_colors_from_map(color_num, map="Spectral"):
cmap = plt.get_cmap(map) # 获取内置colormap
return cmap(np.linspace(0, 1, color_num))
def mountain_plot(data_dict, colors=None):
if colors is None:
colors = get_colors_from_map(len(data_dict), "Spectral")
x = list(data_dict.keys())
# Y轴位置
y_positions = [2 * i for i in range(len(x))]
# 创建图形
fig, axs = plt.subplots(figsize=(8, 12))
# 为每个月绘制核密度曲线,并水平错开显示
for i, month in enumerate(list(data_dict.keys())):
# 核密度估计
density, bins = np.histogram(data_dict[month], bins=30, density=True)
bins = 0.5 * (bins[1:] + bins[:-1]) # 转换为 bin 的中心
# 每个月份的曲线位置偏移
axs.fill_between(bins, y_positions[i] + density, y_positions[i], facecolor=colors[i], alpha=0.7)
axs.plot(bins, y_positions[i] + density, color=colors[i], lw=1.5)
# 设置月份作为Y轴标签
axs.set_yticks(y_positions)
axs.set_yticklabels(x)
# 添加横轴的网格线
axs.grid(axis='y', linewidth=1, color='gray', alpha=0.2)
# 去掉边框线
axs.spines['top'].set_visible(False)
axs.spines['bottom'].set_visible(False)
axs.spines['right'].set_visible(False)
axs.spines['left'].set_visible(False)
# 显示图像
plt.tight_layout()
plt.show()
if __name__ == '__main__':
# 模拟数据生成函数,基于正态分布
def generate_trend_data(size=1000):
np.random.seed(0)
# 前半段平稳
trend = np.linspace(0, 0.3, size // 2)
# 后半段波动较大
trend = np.concatenate([trend, np.random.normal(0.1, 0.5, size // 2)])
return trend
def generate_normal_data(mean, std=1.2, size=1000):
np.random.seed(6) # 固定随机数种子
return np.random.normal(mean, std, size)
# 月份
months = ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec']
# 为每个月生成不同的正态分布数据
data_dict = {}
for i in range(6):
data_dict[months[i]] = generate_normal_data(i * 2) / 10
for i in range(6, 12):
data_dict[months[i]] = generate_normal_data((11 - i) * 2) / 10
mountain_plot(data_dict)图表解读与分析
图表展示:
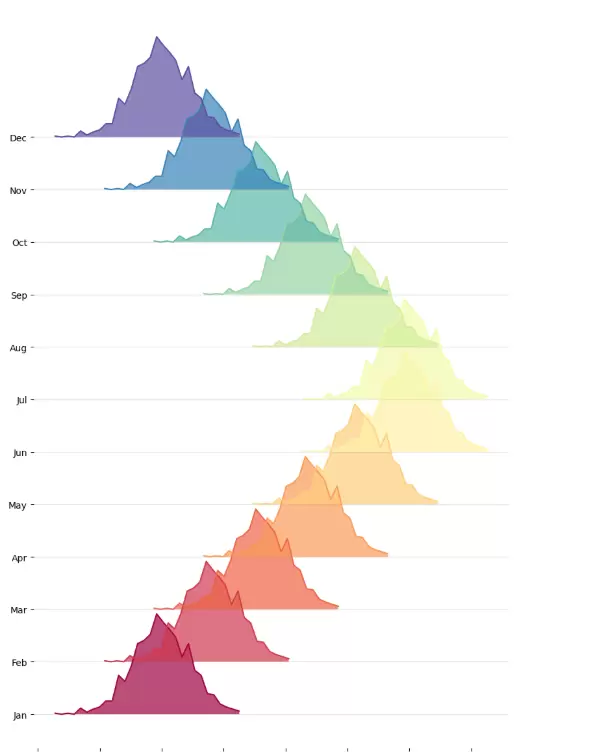
观察生成的山峦图,可以获得以下信息:
- 分布趋势:1 月(Jan)的分布集中在左侧,接着 “山脉” 逐步向右移动,6 月(Jun)到达最右侧,随后再次向左移动,12 月(Dec)回到左侧。这符合我们在模拟数据时 “均值先增后减” 的设计。
- 分布形状:每个月的 “山脉” 宽度体现了数据的离散程度,宽度越大,数据越分散;峰值高度则显示了数据的集中程度,峰值越高,数据越集中。
- 视觉层次:从红色渐变为紫色的色阶,使12 个月的分布在视觉上清晰分开,同时透明度的设定减少了 “山脉” 间的过度遮挡。
山峦图的适用场景与拓展
山峦图适用于以下分析场景:
- 时间序列的分布对比(如每月用户活跃度分布)。
- 不同群体的特性分布对比(如各年龄段的消费金额分布)。
- 实验分组的结果分布对比(如不同实验组的指标分布)。
拓展方向包括:
- 颜色自定义:可根据业务需求更换色阶(如
Viridis
),或对特定类别使用醒目色彩。Plasma - 交互增强:结合
等库,增加悬停提示、缩放等功能。plotly - 多维度融合:在山峦图基础上添加趋势线、统计指标(如均值线),提高信息密度。
山峦图是一种既强大又美观的数据可视化工具,尤其适合展示多组数据的分布状况。相较于传统图表,在展示分布细节和趋势变化方面具有显著优势。借助Matplotlib库,我们能轻松实现此类图表,并根据需求进行多样化的定制。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







