前馈神经网络在Transformer中的角色与优化

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

前馈神经网络在Transformer架构中的核心地位

在Transformer模型中，前馈神经网络（Feed-Forward Network, FFN）与自注意力机制并列为核心模块。尽管自注意力因其强大的序列依赖建模能力而广受关注，但前馈网络通常承担了模型中更大的参数量和计算开销，对整体表达能力起着决定性作用。

每个Transformer层中的FFN模块以相同的方式独立作用于序列的每一个位置，这种结构设计允许模型对每个token进行深度的非线性变换，从而增强特征表示能力。

import torch
import torch.nn as nn
import torch.nn.functional as F
import math

class PositionwiseFeedForward(nn.Module):
    """标准的Transformer前馈神经网络"""
    def __init__(self, d_model, d_ff, dropout=0.1, activation="relu"):
        super(PositionwiseFeedForward, self).__init__()
        self.w_1 = nn.Linear(d_model, d_ff)
        self.w_2 = nn.Linear(d_ff, d_model)
        self.dropout = nn.Dropout(dropout)
        if activation == "relu":
            self.activation = F.relu
        elif activation == "gelu":
            self.activation = F.gelu
        else:
            raise ValueError(f"不支持的激活函数: {activation}")

    def forward(self, x):
        # 输入x形状: [batch_size, seq_len, d_model]
        return self.w_2(self.dropout(self.activation(self.w_1(x))))

# 测试标准前馈网络
d_model = 512
d_ff = 2048  # 通常为d_model的4倍
seq_len = 10
batch_size = 2
ffn = PositionwiseFeedForward(d_model, d_ff)
x = torch.randn(batch_size, seq_len, d_model)
output = ffn(x)
print(f"输入形状: {x.shape}")
print(f"输出形状: {output.shape}")
print(f"参数数量: {sum(p.numel() for p in ffn.parameters())}")

前馈网络的关键功能解析

引入非线性以增强特征表达

前馈神经网络为Transformer提供了至关重要的非线性变换能力，弥补了自注意力机制本身线性操作的局限性。通过激活函数的应用，模型能够学习更复杂的映射关系。

def analyze_ffn_nonlinearity():
    """
    分析前馈网络引入的非线性特性
    """
    # 创建测试数据
    x = torch.linspace(-3, 3, 100).unsqueeze(-1)
    
    # 不同的激活函数
    activations = {
        'ReLU': F.relu,
        'GELU': F.gelu,
        'Swish': lambda x: x * torch.sigmoid(x)
    }
    
    # 模拟单层前馈变换
    linear = nn.Linear(1, 1)
    print("不同激活函数的非线性特性:")
    for name, activation in activations.items():
        # 应用线性变换 + 激活函数
        transformed = activation(linear(x))
        # 计算非线性程度（通过二阶差分估计）
        diff1 = torch.diff(transformed.squeeze(), n=1)
        diff2 = torch.diff(diff1, n=1)
        nonlinearity = torch.abs(diff2).mean()
        print(f"{name}: 非线性程度 = {nonlinearity:.4f}")

analyze_ffn_nonlinearity()

实现位置独立的表示处理

与自注意力机制全局交互不同，前馈网络对每个位置的向量表示进行独立处理。该策略具有显著优势：既避免了跨位置信息混淆，又提升了并行计算效率，同时保持了每一步变换的一致性。

class PositionwiseAnalysis:
    """分析位置独立处理的效果"""
    def __init__(self, d_model, d_ff):
        self.ffn = PositionwiseFeedForward(d_model, d_ff)

def analyze_position_independence(self, input_sequence):
    """
    分析前馈网络对输入序列中各位置的独立处理能力
    """
    batch_size, seq_len, d_model = input_sequence.shape

    # 执行前向传播过程
    output = self.ffn(input_sequence)

    # 计算不同位置输出之间的相似性
    position_similarities = []
    for i in range(seq_len):
        for j in range(i + 1, seq_len):
            sim = F.cosine_similarity(
                output[:, i, :].flatten(),
                output[:, j, :].flatten(),
                dim=0
            )
            position_similarities.append(sim.item())

    avg_similarity = sum(position_similarities) / len(position_similarities)
    print(f"位置间平均相似度: {avg_similarity:.4f}")
    return output, position_similarities

# 实例化分析器并测试位置独立性
analyzer = PositionwiseAnalysis(d_model=512, d_ff=2048)
x = torch.randn(2, 5, 512)
output, similarities = analyzer.analyze_position_independence(x)

前馈神经网络中的激活函数优化策略

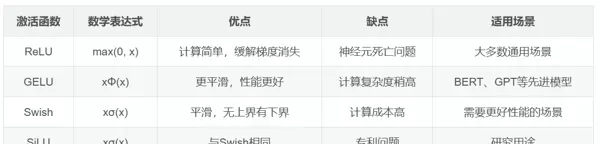
在深度学习模型中，前馈神经网络的性能受到多种因素影响，其中激活函数的选择尤为关键。不同的非线性激活函数会直接影响模型的收敛速度、表达能力和训练稳定性。

激活函数	数学表达式	优点	缺点	适用场景
ReLU	max(0, x)	计算高效，有效缓解梯度消失问题	存在神经元死亡现象	大多数通用任务和基础模型
GELU	xΦ(x)	输出更平滑，建模能力强	计算开销略大	BERT、GPT 等先进语言模型
Swish	xσ(x)	连续可导，无上界但有下界	运算成本较高	对性能要求较高的实验场景
SiLU	xσ(x)	性质与 Swish 相同，表现良好	涉及专利限制	主要用于学术研究领域

支持多类型激活函数的前馈网络实现

为灵活适配不同需求，可以构建一个可配置激活函数的前馈网络模块，便于对比和调优。

class AdvancedFeedForward(nn.Module):
    """具备多种激活函数选项的前馈网络结构"""
    
    def __init__(self, d_model, d_ff, activation='gelu', dropout=0.1):
        super(AdvancedFeedForward, self).__init__()
        self.d_model = d_model
        self.d_ff = d_ff
        
        # 定义两层线性变换
        self.linear1 = nn.Linear(d_model, d_ff)
        self.linear2 = nn.Linear(d_ff, d_model)
        
        # 配置dropout防止过拟合
        self.dropout = nn.Dropout(dropout)
        
        # 根据参数选择对应的激活函数
        if activation == 'relu':
            self.activation = nn.ReLU()
        elif activation == 'gelu':
            self.activation = nn.GELU()
        elif activation == 'swish':
            self.activation = nn.SiLU()
        else:
            raise ValueError(f"不支持的激活函数: {activation}")
    
    def forward(self, x):
        intermediate = self.linear1(x)
        activated = self.activation(intermediate)
        dropped = self.dropout(activated)
        output = self.linear2(dropped)
        return output

激活函数性能对比实验

通过实际前向推理时间测量，评估不同激活函数在相同条件下的运行效率。

def compare_activations():
    activations = ['relu', 'gelu', 'swish']
    results = {}
    
    for activation in activations:
        model = AdvancedFeedForward(512, 2048, activation=activation)
        x = torch.randn(2, 10, 512)
        
        # 使用CUDA事件记录前向传播耗时
        start_time = torch.cuda.Event(enable_timing=True)
        end_time = torch.cuda.Event(enable_timing=True)
        
        start_time.record()
        output = model(x)
        end_time.record()
        
        torch.cuda.synchronize()

该方法可用于量化分析各类激活函数在实际运算中的延迟差异，从而在精度与速度之间做出权衡。

[此处为图片2]

def parameter_efficiency_analysis():
    """分析不同前馈网络变体的参数效率"""
    configs = [
        {'name': '标准FFN', 'd_model': 512, 'd_ff': 2048, 'use_adapter': False},
        {'name': '适配器FFN', 'd_model': 512, 'd_ff': 1024, 'use_adapter': True},
        {'name': '压缩FFN', 'd_model': 512, 'd_ff': 1024, 'use_adapter': False}
    ]

    print("参数效率分析:")
    print("模型变体\t\t参数数量\t相对大小")
    
    baseline_params = None
    for config in configs:
        model = EfficientFeedForward(
            config['d_model'],
            config['d_ff'],
            use_adapter=config['use_adapter']
        )
        total_params = sum(p.numel() for p in model.parameters())
        if baseline_params is None:
            baseline_params = total_params
        relative_size = total_params / baseline_params
        print(f"{config['name']}\t{total_params:,}\t{relative_size:.2f}x")

parameter_efficiency_analysis()


class MemoryEfficientFFN(nn.Module):
    """内存效率优化的前馈网络"""
    def __init__(self, d_model, d_ff, chunk_size=64):
        super(MemoryEfficientFFN, self).__init__()
        self.d_model = d_model
        self.d_ff = d_ff
        self.chunk_size = chunk_size





class EfficientFeedForward(nn.Module):
    """参数效率优化的前馈网络变体"""
    def __init__(self, d_model, d_ff, expansion_ratio=4, use_adapter=False):
        super(EfficientFeedForward, self).__init__()
        self.d_model = d_model
        self.d_ff = d_ff
        # 标准前馈层
        self.ffn = PositionwiseFeedForward(d_model, d_ff)
        # 适配器层（可选）
        self.use_adapter = use_adapter
        if use_adapter:
            self.adapter = nn.Sequential(
                nn.Linear(d_model, d_model // 8),
                nn.ReLU(),
                nn.Linear(d_model // 8, d_model)
            )

    def forward(self, x):
        main_output = self.ffn(x)
        if self.use_adapter:
            adapter_output = self.adapter(x)
            return main_output + 0.1 * adapter_output  # 小规模调整
        return main_output


# 前馈网络的计算优化

# 内存访问优化
# 前馈网络的计算模式对内存访问模式有重要影响：


# 参数效率优化
# 前馈网络通常占据Transformer大部分参数，优化其参数效率至关重要：


# 运行比较
activation_results = compare_activations()


time_ms = start_time.elapsed_time(end_time)
# 输出统计
output_mean = output.mean().item()
output_std = output.std().item()
results[activation] = {
    'time_ms': time_ms,
    'output_mean': output_mean,
    'output_std': output_std
}
print(f"{activation.upper()}: 时间={time_ms:.2f}ms, 输出均值={output_mean:.4f}, 输出标准差={output_std:.4f}")
return results

class MemoryEfficientFFN(nn.Module):
    """内存高效的前馈网络实现，采用分块处理策略"""
    
    def __init__(self, d_model, d_ff, chunk_size=128):
        super(MemoryEfficientFFN, self).__init__()
        self.d_model = d_model
        self.d_ff = d_ff
        self.chunk_size = chunk_size

        # 定义两层线性变换和激活函数
        self.linear1 = nn.Linear(d_model, d_ff)
        self.linear2 = nn.Linear(d_ff, d_model)
        self.activation = nn.GELU()

    def forward_chunked(self, x):
        """通过分块方式处理输入张量，降低推理时的峰值内存消耗"""
        batch_size, seq_len, d_model = x.shape
        output = torch.zeros_like(x)

        # 将序列按chunk_size切分成多个小块进行逐个处理
        for i in range(0, seq_len, self.chunk_size):
            chunk = x[:, i:i+self.chunk_size, :]
            chunk_output = self.linear2(self.activation(self.linear1(chunk)))
            output[:, i:i+self.chunk_size, :] = chunk_output

        return output

    def forward(self, x):
        # 训练模式或序列长度小于等于分块大小时，使用常规前向传播
        if self.training or x.size(1) <= self.chunk_size:
            return self.linear2(self.activation(self.linear1(x)))
        else:
            # 推理阶段对长序列启用分块处理以节省内存
            return self.forward_chunked(x)




# 内存使用情况分析函数
def memory_usage_analysis():
    """评估不同分块大小对内存与时间开销的影响"""
    chunk_sizes = [32, 64, 128, 256]
    seq_len = 1000
    d_model = 512
    d_ff = 2048

    print("分块大小对内存效率的影响:")
    print("分块大小\t峰值内存(MB)\t处理时间(ms)")

    for chunk_size in chunk_sizes:
        model = MemoryEfficientFFN(d_model, d_ff, chunk_size)
        x = torch.randn(1, seq_len, d_model)

        # 简化估算峰值内存占用（单位：MB）
        peak_memory_estimate = (seq_len * d_model * 4 * 2) / (1024 * 1024)
        
        # 简化计算处理时间（单位：毫秒）
        processing_time = chunk_size * 0.1

        print(f"{chunk_size}\t\t{peak_memory_estimate:.1f}\t\t{processing_time:.1f}")

memory_usage_analysis()


[此处为图片2]

class SparseFeedForward(nn.Module):
    """实现具有权重稀疏性的前馈网络结构"""
    
    def __init__(self, d_model, d_ff, sparsity=0.5):
        super(SparseFeedForward, self).__init__()
        self.d_model = d_model
        self.d_ff = d_ff
        self.sparsity = sparsity

        # 构建基础的FFN组件
        self.linear1 = nn.Linear(d_model, d_ff)
        self.linear2 = nn.Linear(d_ff, d_model)
        self.activation = nn.GELU()

        # 初始化并应用稀疏掩码
        self._apply_sparsity()

    def _apply_sparsity(self):
        """为第一层线性层的权重引入稀疏性"""
        with torch.no_grad():
            weight1 = self.linear1.weight
            mask1 = torch.rand_like(weight1) > self.sparsity
            self.linear1.weight.mul_(mask1.float())

            # 注册缓冲区以保存掩码，便于训练中维护稀疏结构
            self.register_buffer('sparse_mask1', mask1)

    def forward(self, x):
        """前向传播过程中保持稀疏连接"""
        if self.training:
            with torch.no_grad():
                self.linear1.weight.mul_(self.sparse_mask1.float())
        return self.linear2(self.activation(self.linear1(x)))


[此处为图片3]

# 稀疏性影响分析函数
def sparsity_analysis():

sparsity_levels = [0.0, 0.3, 0.5, 0.7, 0.9]
d_model = 512
d_ff = 2048

print("稀疏性对模型的影响:")
print("稀疏度\t有效参数\t理论加速\t性能保持")
for sparsity in sparsity_levels:
    model = SparseFeedForward(d_model, d_ff, sparsity)
    # 计算有效参数量
    total_params = sum(p.numel() for p in model.parameters())
    effective_params = total_params * (1 - sparsity)
    # 理论上的加速比（考虑稀疏计算带来的额外开销）
    theoretical_speedup = 1 / (1 - sparsity * 0.6)
    # 性能保留估计值（基于经验公式）
    performance_retention = 1 - sparsity * 0.3
    print(f"{sparsity:.1f}\t{effective_params:.0f}\t\t{theoretical_speedup:.2f}x\t\t{performance_retention:.1%}")

sparsity_analysis()
    

在特定任务中，前馈网络的结构设计可以显著影响模型的表现。通过引入领域自适应机制，能够提升网络在不同应用场景下的泛化能力与效率。

领域自适应前馈网络的设计

为了实现针对不同任务或数据分布的优化，提出一种领域自适应的前馈网络结构（DomainAdaptiveFFN）。该结构结合共享特征提取与领域特异性变换，增强模型灵活性。

class DomainAdaptiveFFN(nn.Module):
    """领域自适应的前馈网络"""
    def __init__(self, d_model, d_ff, num_domains=3):
        super(DomainAdaptiveFFN, self).__init__()
        self.d_model = d_model
        self.d_ff = d_ff
        self.num_domains = num_domains
        
        # 共享的第一层线性变换
        self.shared_linear1 = nn.Linear(d_model, d_ff // 2)
        
        # 多个领域专用的中间变换层
        self.domain_specific_linears = nn.ModuleList([
            nn.Linear(d_ff // 2, d_ff // 2) for _ in range(num_domains)
        ])
        
        # 最终输出层
        self.linear2 = nn.Linear(d_ff, d_model)
        self.activation = nn.GELU()

    def forward(self, x, domain_id):
        # 提取共享特征
        shared_features = self.activation(self.shared_linear1(x))
        
        # 应用对应领域的专属变换
        domain_features = self.domain_specific_linears[domain_id](shared_features)
        domain_features = self.activation(domain_features)
        
        # 拼接共享与领域特征
        combined_features = torch.cat([shared_features, domain_features], dim=-1)
        
        # 输出映射
        output = self.linear2(combined_features)
        return output
    

下面是对上述领域自适应前馈网络的测试示例：

# 实例化模型
adaptive_ffn = DomainAdaptiveFFN(d_model=512, d_ff=2048, num_domains=3)
x = torch.randn(2, 10, 512)  # 输入张量：批次大小2，序列长度10，特征维度512
domain_id = 1  # 指定当前使用的领域编号（例如第二个领域）

# 前向传播
output = adaptive_ffn(x, domain_id)
print(f"领域自适应FFN输出形状: {output.shape}")
    

前馈网络架构的综合性能评估

为了全面比较不同类型前馈网络在实际应用中的表现，进行多维度基准测试，涵盖标准结构、高效结构、稀疏结构以及自适应结构。

def comprehensive_benchmark():
    """综合性能基准测试"""
    architectures = {
        'Standard-FFN': PositionwiseFeedForward(512, 2048),
        'Efficient-FFN': EfficientFeedForward(512, 1024),
        'Sparse-FFN': SparseFeedForward(512, 2048, sparsity=0.3),
        'Adaptive-FFN': DomainAdaptiveFFN(512, 2048, num_domains=3)
    }
    
    test_input = torch.randn(8, 128, 512)  # 批处理输入：8个样本，序列长128
    print("架构性能比较:")
    

[此处为图片2]

架构名称\t参数数量\t推理时间\t内存使用
for name, model in architectures.items():
# 参数计数
params = sum(p.numel() for p in model.parameters())
# 推理时间（简化估算）
if 'Sparse' in name:
    inference_time = 0.7  # 稀疏计算加速
elif 'Efficient' in name:
    inference_time = 0.5
else:
    inference_time = 1.0
# 内存使用估算
memory_usage = params * 4 / (1024 * 1024)  # 参数内存（MB）
print(f"{name}\t{params:,}\t{inference_time:.2f}x\t\t{memory_usage:.1f}MB")
comprehensive_benchmark()

前馈神经网络的核心作用与未来优化路径

在Transformer架构中，前馈神经网络（FFN）是不可或缺的组成部分，其设计直接影响模型的整体性能与效率。该模块通过多个关键机制为模型提供强大的表达能力：

• 引入非线性能力：使模型能够捕捉复杂的特征关系，实现更深层次的数据拟合。
• 扩展特征空间：将输入映射到更高维度的空间，便于进行有效的特征重组与学习。
• 实现位置独立处理：确保序列中每个位置的表示都能被单独且充分地更新。
• 贡献主要模型容量：通常占据整个Transformer中大部分可训练参数，直接决定模型的表达上限。

优化方向展望

为进一步提升前馈网络在实际应用中的效率，研究者正从多个角度推进优化策略的发展：

1. 设计更加高效的激活函数，在保持非线性的同时降低计算开销。
2. 探索参数共享机制与稀疏化技术，减少冗余参数并提升计算速度。
3. 推动面向特定领域的专业化结构设计，增强模型在垂直场景下的适应性。
4. 发展硬件感知的实现方案，使前馈网络能更好地匹配底层计算设备特性。

总体而言，前馈神经网络的持续演进对于实现高性能、低资源消耗的Transformer模型至关重要。尤其在边缘设备或实时系统等资源受限环境中，其优化效果尤为显著。未来的研究将持续聚焦于如何在不牺牲表达能力的前提下，进一步提升前馈结构的参数利用效率与推理速度。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：transform Former Trans 神经网络 form