发帖
雷达卡
第一部分：核心概念解析
导数反映的是函数在某一特定点上的瞬时变化速率，也就是因变量随着自变量的微小变动而产生的即时响应程度。
从数学极限的角度来看，对于一个函数 y=f(x)，其在某点 x 处的导数可由以下极限表达式定义：
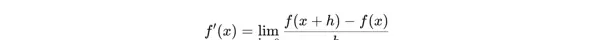
这一表达式本质上是“平均变化率”在两个点无限趋近于彼此时所取得的极限值。
第二部分：常用计算方法与规则
在实际操作中，通常不会每次都通过极限定义来求导，而是依赖已知的导数公式和运算法则进行快速计算。
基本初等函数的导数公式
这些公式构成了导数运算的基础，掌握它们是进一步计算的前提。
导数的四则与复合运算法则
当函数形式较为复杂时，需依据其结构选择合适的求导法则。常见的包括和差、乘积、商以及复合函数的求导规则。
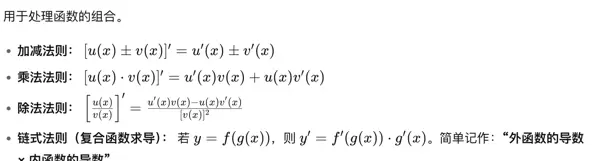
第三部分：实例演示与数值计算
通过具体例题可以更直观地理解导数的计算过程及其结果的意义。
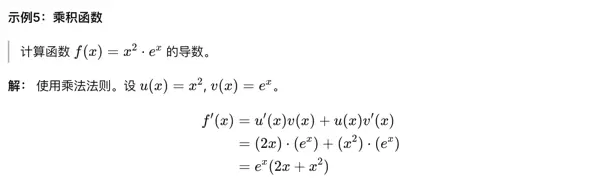
第四部分：导数的实际应用与数据分析
导数不仅是一个理论工具，在实际问题中也具有广泛的解释能力，例如用于分析增长趋势、极值判断、曲线斜率等。
总结与学习建议
要熟练掌握导数的计算，应重点关注以下几点：
- 牢固记忆基本初等函数的导数公式；
- 准确识别目标函数的构成形式（如是否为乘积、分式或复合结构）；
- 合理选用对应的求导法则，并分步实施计算。
从这些基础出发，绝大多数常见初等函数的导数都可以被有效求解。
京公网安备 11010802022788号
