一、理论基础
1.1 等值线的数学定义与可视化意义
在二维空间中,等值线是连接具有相同数值点的曲线。这一概念广泛应用于数据可视化领域,用于表现函数 z = f(x, y) 在平面上满足 f(x, y) = c(c 为常数)的所有点构成的轨迹。其核心思想源于地图学中的“等高线”,即表示相同海拔高度的闭合曲线。
1.2 标量场与梯度特性
等值线图建立在以下三个关键数学概念之上:
- 标量场:每个坐标点 (x, y) 对应一个确定的数值 z,形成一个二维数值分布。
- 等值线:将所有 z 值相等的点连接而成的曲线,反映数值的等量区域。
- 梯度属性:函数变化最快的方向垂直于等值线,而线密度越高,表示变化越剧烈。
contour()contourf()1.3 Matplotlib 中的核心绘图函数
Matplotlib 提供了两类主要函数用于绘制等值线结构:
contour():生成轮廓线,仅描绘边界而不填充颜色。contourf():实现区域填充,增强视觉层次感,适用于连续场强展示。
1.4 主要参数解析
常用配置项包括:
- X, Y:定义网格坐标的二维数组。
- Z:对应每个 (x, y) 位置的数值矩阵。
- levels:控制等值线的数量或具体取值层级。
- colors:设定线条颜色,支持单色或多色列表。
- linewidths:调整线宽以突出重要层级。
- linestyles:定义实线、虚线等样式。
- cmap:指定色彩映射方案,常用于填充图的颜色渐变。
二、实际应用示例
2.1 基础等高线图示
该图呈现标准黑白轮廓结构,未进行色彩填充,线条平滑且标注清晰。最外圈标记 ±0.15,向内逐级递增(正向:0.30 → 0.90;负向:-0.30 → -0.90),中心分别对应峰值 +0.9 和谷值 -0.9。数值直接标注在线条旁,便于读取。坐标范围从 -4 到 +4,无单位标识,整体布局对称,展现单一峰谷结构的俯视效果。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans Fallback']
plt.rcParams['axes.unicode_minus'] = False
# 创建数据
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
# 定义一个函数:z = sin(x) * cos(y)
Z = np.sin(X) * np.cos(Y)
# 创建图形
plt.figure(figsize=(10, 8))
# 绘制等高线
contour = plt.contour(X, Y, Z, levels=15, colors='black', linewidths=0.8)
# 添加等高线标签
plt.clabel(contour, inline=True, fontsize=8)
# 添加标题和标签
plt.title('基础等高线图示例', fontsize=16, fontweight='bold')
plt.xlabel('X轴', fontsize=12)
plt.ylabel('Y轴', fontsize=12)
# 显示图形
plt.grid(True, alpha=0.3)
plt.tight_layout() # 自动调整布局,防止标签被裁剪
plt.show()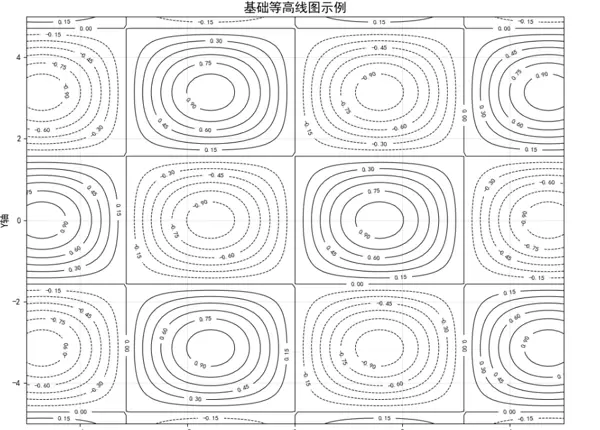
2.2 填充型等值线图
此图为典型的二维高斯分布可视化结果,采用渐变色填充方式呈现。中心最大值达 0.9,显示为亮黄色;向外依次过渡为青绿、深青,最终至边缘变为深蓝,表示数值趋近于零。色带之间过渡自然,无黑色边框,边界柔和。坐标轴范围为 -3 至 +3,呈对称指数衰减形态,突显出位于图像中央的主峰特征。
简言之,这是一幅用色彩浓淡表达高低起伏的“彩色地形图”,直观揭示出峰值所在位置——正中央。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
# 方法1:尝试使用系统字体(Windows系统)
try:
# 尝试几种常见的中文字体
font_paths = [
'C:/Windows/Fonts/simhei.ttf', # 黑体
'C:/Windows/Fonts/msyh.ttc', # 微软雅黑
'C:/Windows/Fonts/simsun.ttc', # 宋体
'C:/Windows/Fonts/simkai.ttf', # 楷体
]
for font_path in font_paths:
try:
font_prop = matplotlib.font_manager.FontProperties(fname=font_path)
matplotlib.font_manager.fontManager.addfont(font_path)
font_name = matplotlib.font_manager.FontProperties(fname=font_path).get_name()
plt.rcParams['font.sans-serif'] = [font_name]
plt.rcParams['axes.unicode_minus'] = False
print(f"成功加载字体: {font_name}")
break
except:
continue
else:
# 如果所有指定字体都失败,使用回退方案
print("使用回退字体方案")
plt.rcParams['font.sans-serif'] = ['DejaVu Sans', 'SimHei', 'Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
except Exception as e:
print(f"字体加载异常: {e}")
# 设置通用回退
plt.rcParams['font.sans-serif'] = ['DejaVu Sans', 'SimHei', 'Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 创建数据
x = np.linspace(-3, 3, 50)
y = np.linspace(-3, 3, 50)
X, Y = np.meshgrid(x, y)
# 定义一个高斯函数
Z = np.exp(-(X**2 + Y**2))
# 创建图形
plt.figure(figsize=(10, 8))
# 绘制填充等高线
contourf = plt.contourf(X, Y, Z, levels=20, cmap='viridis')
# 添加颜色条
plt.colorbar(contourf, label='高度值')
# 添加标题和标签
plt.title('填充等高线图 - 高斯分布', fontsize=16, fontweight='bold')
plt.xlabel('X轴', fontsize=12)
plt.ylabel('Y轴', fontsize=12)
# 显示图形
plt.tight_layout()
plt.show()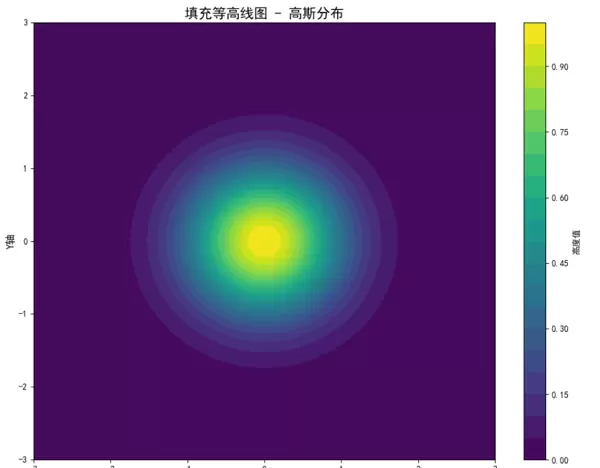
2.3 复合式等值线展示
图像由两层信息叠加构成:
- 底层使用连续渐变色块,从深蓝(最低点 –1.8)过渡至亮黄(最高点 +1.8),类似热力图表现手法。
- 上层叠加 30 条黑色细线,每间隔约 0.09 单位绘制一条等值线,形成闭合环路。线密度反映坡度变化:密集处变化剧烈,稀疏区则趋于平缓。
整体视觉如同一张被揉皱的金属薄片:
- 右中部存在显著“热点”,接近 +1.8,呈明亮黄色。
- 左下与右上各有一处深蓝色洼地,降至 –1.8。
- 中间区域颜色交替频繁,黑线交错密集,表明函数在此区间波动强烈。
坐标跨度为 –4 到 +4,虽对称但无规则几何形态,体现出复杂非线性函数的典型特征——多峰共存、高低错落。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
# 方法1:直接使用黑体(Windows系统通常都有)
try:
# 添加黑体字体
font_path = 'C:/Windows/Fonts/simhei.ttf'
font_prop = matplotlib.font_manager.FontProperties(fname=font_path)
matplotlib.font_manager.fontManager.addfont(font_path)
font_name = matplotlib.font_manager.FontProperties(fname=font_path).get_name()
# 设置全局字体
plt.rcParams['font.sans-serif'] = [font_name]
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.size'] = 12
print(f"成功加载字体: {font_name}")
except Exception as e:
print(f"加载黑体失败: {e}")
# 尝试其他字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
# 创建数据
x = np.linspace(-2*np.pi, 2*np.pi, 100)
y = np.linspace(-2*np.pi, 2*np.pi, 100)
X, Y = np.meshgrid(x, y)
# 定义一个复杂函数
Z = np.sin(X) * np.cos(Y) + np.sin(2*X) * np.cos(2*Y)
# 创建图形
plt.figure(figsize=(12, 8))
# 绘制填充等高线
contourf = plt.contourf(X, Y, Z, levels=30, cmap='RdYlBu', alpha=0.8)
# 绘制等高线轮廓
contour = plt.contour(X, Y, Z, levels=30, colors='black', linewidths=0.5, alpha=0.8)
# 添加颜色条
plt.colorbar(contourf, label='函数值')
# 添加标题和标签
plt.title('组合等高线图 - 复杂函数', fontsize=16, fontweight='bold')
plt.xlabel('X轴', fontsize=12)
plt.ylabel('Y轴', fontsize=12)
# 设置坐标轴范围
plt.xlim(-2*np.pi, 2*np.pi)
plt.ylim(-2*np.pi, 2*np.pi)
# 显示图形
plt.tight_layout()
plt.show()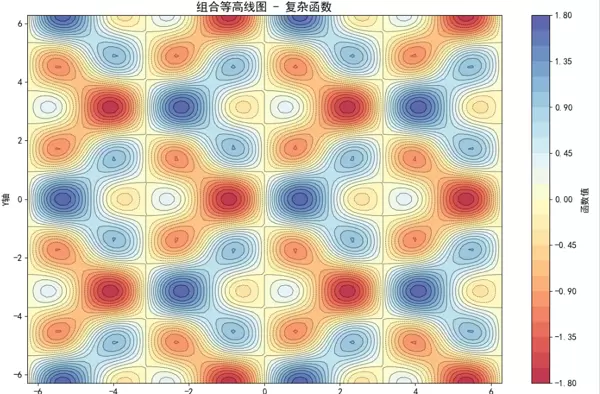
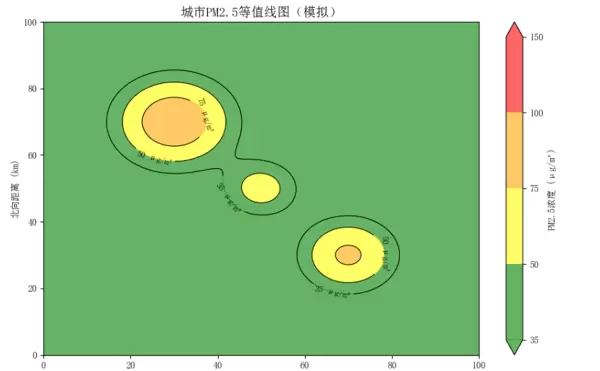
2.4 环境监测实例:城市PM2.5浓度分布
本图模拟一座 100 km × 100 km 范围的城市空气污染状况,通过颜色与等值线结合的方式构建“烟雾地形”。外围为绿色带,对应浓度 35 ?g/m?,代表空气质量良好区域;向内颜色逐步转暖,依次出现黄、橙、红、紫色区块,分别对应 50、75、100、150 ?g/m? 的污染等级。
三条黑色闭合线明确划分出不同污染水平,并在线上直接标注“50”“75”“100”,方便快速识别。
图中可见三处主要污染源:
- 西北部出现深红色聚集区,形似烟囱排放口。
- 东南角有大片紫色斑块,浓度高达 150 ?g/m?,是最严重的“污染坑”。
- 市中心周围环绕橙色区域,说明日常排放导致 75 ?g/m? 浓度范围广泛。
三、等高线与等值线的关系辨析
“等高线”特指地形高度这一类标量场,即将海拔相同的地理点连成闭合曲线,单位统一为米。例如地图中标注为 500 的棕色环线,意味着沿该线行走时,地面始终处于海拔 500 米的高度。
而“等值线”是一个更广义的概念,泛指任何二维标量场中数值相等的轨迹集合。其所代表的物理量不限于高度,可涵盖温度、气压、污染物浓度、噪声强度、人口密度等多种变量,单位也随应用场景灵活变化。如 30℃ 等温线、1013 hPa 等压线、75 ?g/m? PM2.5 浓度线,本质上均为等值线的具体形式。
区别在于:前者专用于地形描述,后者适用于一切“数值相等”的空间分布表达。因此可以总结为:所有等高线都是等值线的一种,但并非所有等值线都是等高线。
四、典型应用场景
等值线技术已被广泛应用于多个科学与工程领域,尤其适合需要直观展现二维标量场中“等量区域”的场景。
地理信息系统(GIS)
用于地形建模,通过等高线精确表达地表起伏状态,辅助路径规划与地貌分析。
气象与海洋学
除常见的气温、气压分布外,还可绘制露点、湿度、风速、海表温度、盐度及有效波高等多种要素的等值线图,提升天气预报与气候研究精度。
环境监测
用于空气质量评估,如 PM?.?、O?、SO?、NO? 等污染物浓度的空间分布;也可用于土壤重金属含量、水体溶解氧、叶绿素浓度、浊度以及噪声 dB(A) 等响线的制图分析。
工程与物理仿真
在应力分析、流体力学等领域,利用等值线可视化压力、速度、温度等场量分布,帮助识别热点区域与异常梯度。
机器学习与优化
在损失函数的参数空间中绘制等值线,有助于理解模型收敛路径与局部极小值分布。
金融建模
用于波动率曲面、期权价格或风险敞口的空间展示,辅助投资决策。
综上所述,只要存在一个可表示为 Z(x, y) 的二维数值函数,即可借助等值线将其转化为可视化的等量边界图谱。因其通用性强,远比局限于地形的“等高线”更具适应性和扩展性。
在数据可视化领域,等高线图是一种极为有效的工具,能够清晰呈现二维空间中数值的变化趋势与分布规律。例如,在医学成像中,CT或MRI图像中的亨氏单位等密度线可用于反映组织密度差异;在神经科学中,脑电图的电位等势线有助于揭示大脑活动的空间分布;皮肤温度的等温线则能直观显示体表热分布情况;而在放射治疗的剂量规划过程中,等剂量线对于评估辐射能量的空间覆盖至关重要。

借助Matplotlib这一功能强大的绘图库,用户可以灵活生成多种类型的等高线图——无论是基础的轮廓线条图,还是带有色彩填充的区域图,亦或是扩展至三维空间的曲面表示,均可高效实现。这些图形不仅提升了数据的表现力,也增强了分析的直观性。
综上所述,掌握等高线图的绘制方法,对于深入理解复杂二维数据的结构特征具有重要意义。无论是在科研、医疗还是工程领域,这类图形都发挥着不可替代的作用,是数据分析过程中不可或缺的可视化手段。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







