EKF：基于MATLAB Similink的扩展卡尔曼滤波器EKF的锂电池SoC计算仿真模型

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

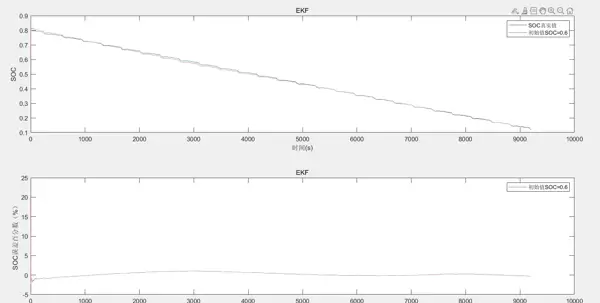
最近在进行锂电池SoC估算相关的项目时，发现扩展卡尔曼滤波（EKF）是一种非常有效的算法。相比传统安时积分法会累积误差、开路电压法无法实时测量的问题，EKF能够有效融合两者优势，实现更精确的实时状态估计。本文将详细介绍如何基于MATLAB/Simulink搭建用于锂电池SoC估算的EKF仿真模型，并分享关键参数调试的经验与避坑建议。 首先，电池等效电路模型的选择至关重要。目前应用较广的是二阶RC等效电路模型，因其在计算复杂度和建模精度之间取得了良好平衡。该模型可在Simulink中构建如下结构：

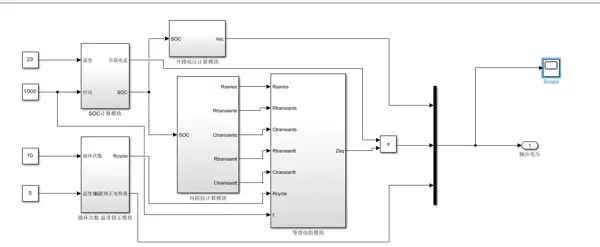
% 电池模型参数定义
R0 = 0.01;   % 欧姆内阻
Rp1 = 0.005; % 极化电阻1
Cp1 = 2000;  % 极化电容1 
Rp2 = 0.008; % 极化电阻2
Cp2 = 1500;  % 极化电容2

在搭建过程中需特别注意：RC环节的时间常数必须与实际电池动态特性相匹配，不能随意设定。推荐先通过HPPC测试获取真实电池数据，再利用系统辨识方法拟合模型参数，以提高仿真可靠性。若直接凭经验赋值，极易导致模型失真。 接下来是EKF的核心部分——状态方程设计。在此模型中，SoC被作为系统的隐藏状态变量，需与非线性观测量协同处理：

function [x_k, F_k] = stateFcn(x_prev, I, deltaT, Cn)
    x_k = x_prev - (deltaT/Cn)*I;  % SoC状态递推
    F_k = 1;  % 状态转移矩阵雅可比
end

其中，deltaT表示采样时间间隔，Cn为电池额定容量。在计算雅可比矩阵时，务必确保单位统一。例如，曾有案例因未将分钟转换为秒，导致SoC估算曲线严重偏离正常范围。 关于观测方程的设计，需要准确描述端电压与SoC之间的非线性关系。以下以三元锂电池为例，采用包含指数项的OCV-SoC函数来刻画两端区间的陡变特性：

function [V_est, H_k] = measFcn(x_k, I, R0, Rp1, Cp1, Rp2, Cp2)
    ocv = 3.7 + 0.6*x_k - 0.2*exp(-15*x_k);  % 典型OCV拟合公式
    V_est = ocv - I*(R0 + Rp1/(1+Rp1*Cp1) + Rp2/(1+Rp2*Cp2));
    H_k = 0.6 + 3*exp(-15*x_k);  % 对SoC求导得到观测矩阵
end

为了提升拟合精度，建议对实测OCV-SoC数据进行三次样条插值处理。此外，过程噪声协方差Q和观测噪声协方差R的设置较为敏感，初始值可设为1e-6量级。若数值过大，系统容易出现振荡；过小则收敛速度缓慢，影响实时性。 完整的Simulink模型主要包括以下几个模块： - 电池物理行为子系统 - 添加噪声的电流与电压传感器模块 - 基于MATLAB Function封装的EKF算法核心 - 实时SoC可视化显示单元 值得注意的是，不建议直接使用Simulink官方提供的EKF模块，自行搭建更具灵活性且便于调试。 若仿真结果呈现类似心电图的剧烈波动，大概率是雅可比矩阵推导或编码出错。例如，曾有一次误将极化电阻Rp1与Rp2位置颠倒，导致SoC估计超前真实值约20%，耗时两天排查才发现问题出在观测方程中的电阻顺序错误。 在验证阶段，应优先使用0.2C以下的小电流工况进行实测对比，避免大电流引入显著模型误差。推荐将安时积分法的结果与EKF输出绘制在同一图表中，当偏差持续超过5%时，应及时检查模型结构及参数设置是否合理。 最后，在代码集成时应预留温度补偿接口。实际应用中，电池工作温度的变化会对RC参数产生显著影响，远比恒温仿真的情况复杂。未来还可进一步探索自适应EKF与神经网络的融合策略，这类方法更贴近工业级工程需求。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：扩展卡尔曼滤波 卡尔曼滤波器 MATLAB 卡尔曼滤波 matla

相关内容：Matlab模型仿真