线性与非线性MPC控制的四旋翼轨迹跟踪仿真对比研究
在四旋翼飞行器控制系统中,轨迹跟踪性能是衡量控制器有效性的重要指标。模型预测控制(MPC)凭借其对系统动态特性的显式建模能力以及对输入和状态约束的良好处理机制,成为实现高精度轨迹跟踪的有效方法之一。本文重点围绕基于线性化与非线性动力学模型的MPC控制器设计,开展仿真对比分析,探讨二者在轨迹跟踪表现上的差异。
四旋翼动力学建模与状态空间表示
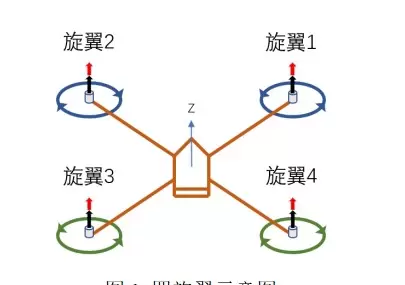
为实施模型预测控制,首先需建立准确描述四旋翼运动行为的动力学模型,并将其转化为适用于MPC框架的状态空间形式。该过程包括构建非线性模型及其在平衡点附近的线性近似模型,形成多输入多输出(MIMO)系统结构。
非线性动力学模型构建
四旋翼系统的非线性特性源于其在三维空间中的强耦合运动关系。基于牛顿-欧拉方程,可得其完整的非线性动力学表达式:
\[ \begin{cases} m\ddot{x} = -T\sin\theta\cos\psi \\ m\ddot{y} = T\sin\theta\sin\psi \\ m\ddot{z} = T\cos\theta - mg \\ I_x\ddot{\phi} = (\tau_\phi + I_{xz}(\dot{\theta}\dot{\psi}\cos\phi - \ddot{\theta}\sin\phi)) \\ I_y\ddot{\theta} = (\tau_\theta + I_{xz}(\dot{\phi}\dot{\psi}\sin\phi + \ddot{\phi}\cos\phi)) \\ I_z\ddot{\psi} = \tau_\psi \end{cases} \]
其中,$ m $ 表示飞行器质量,$ T $ 为总推力,$ \tau_\phi, \tau_\theta, \tau_\psi $ 分别代表滚转、俯仰和偏航方向的控制力矩;$ I_x, I_y, I_z $ 为各轴转动惯量,$ I_{xz} $ 为惯性积项。此模型完整反映了位置与姿态变量之间的非线性耦合关系,适用于高精度仿真与非线性控制器设计。

线性化状态空间模型推导
为简化控制器设计流程,通常在悬停平衡点附近对非线性模型进行局部线性化处理。假设飞行器处于小角度姿态运行状态(即 $ \phi, \theta \approx 0 $),且角速度变化缓慢,通过泰勒展开并忽略高阶非线性项,可获得如下线性时不变(LTI)状态空间模型:
\[ \dot{\mathbf{x}} = \mathbf{A}\mathbf{x} + \mathbf{B}\mathbf{u} \]其中,状态向量定义为 $ \mathbf{x} = [x, y, z, \dot{x}, \dot{y}, \dot{z}, \phi, \theta, \psi, \dot{\phi}, \dot{\theta}, \dot{\psi}]^T $,控制输入向量取为 $ \mathbf{u} = [\omega_1^2, \omega_2^2, \omega_3^2, \omega_4^2]^T $,分别对应四个电机转速平方值。矩阵 $ \mathbf{A} $ 和 $ \mathbf{B} $ 由系统参数及线性化条件确定,便于后续用于线性MPC算法实现。
MPC控制器设计原理与实现
模型预测控制的核心在于利用当前状态和系统模型对未来一段时间内的系统行为进行滚动预测,并通过求解优化问题来生成最优控制序列,使实际轨迹尽可能逼近参考路径,同时满足物理约束条件。
状态空间模型在MPC中的应用转化
为了适配MPC算法结构,必须将原始动力学方程转换为离散化或连续化的状态空间格式。对于线性MPC而言,上述已推导出的线性状态空间模型可直接代入预测公式;而对于非线性MPC,则需保留原始非线性微分方程作为预测模型,在每个控制周期内在线求解非线性优化问题。
线性MPC算法推导与预测机制
在线性MPC框架下,控制目标是在每一采样时刻 $ k $ 求解一个有限时域的二次规划(QP)问题,以最小化跟踪误差并满足控制输入约束。设预测时域为 $ N_p $,控制时域为 $ N_c $(满足 $ N_c \leq N_p $),则状态预测方程可表示为:
\[ \mathbf{X}_{k+1|k} = \mathbf{A}\mathbf{X}_{k|k} + \mathbf{B}\mathbf{U}_{k|k} \]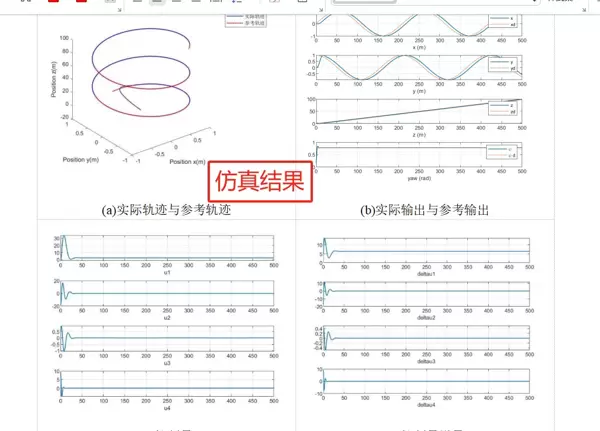
该递推关系用于构建未来状态序列的显式表达式,进而构造包含跟踪误差与控制增量的代价函数。通过对该优化问题的实时求解,获取当前时刻的最佳控制动作,并执行首项控制指令,随后在下一时刻重复该过程,实现滚动优化控制。
非线性MPC算法设计思路
相较于线性MPC,非线性MPC采用原始非线性模型进行预测,能够更精确地刻画系统动态,尤其适用于大机动飞行或存在显著非线性效应的场景。其优化问题通常表现为非线性规划(NLP),需借助如SQP、IPOPT等数值求解器完成。虽然计算负担较重,但其控制精度和鲁棒性往往优于线性方案。
仿真分析与对比总结
通过搭建MATLAB/Simulink或Python环境下仿真平台,分别实现线性与非线性MPC控制器对典型轨迹(如八字形、正弦曲线等)的跟踪测试。评估指标包括跟踪误差均方根(RMSE)、控制输入平滑性、实时计算耗时等。
结果表明:在线性工作区域内,线性MPC具有良好的控制性能与较低的计算开销,适合嵌入式部署;而在强非线性或快速机动条件下,非线性MPC展现出更优的轨迹贴合能力,尽管牺牲了一定的实时性。
综上所述,两种方法各有优势,选择应根据具体应用场景、硬件资源与控制需求综合权衡。
在模型预测控制(MPC)中,优化目标通常设定为最小化系统预测输出与期望轨迹之间的偏差,同时对控制输入的变化施加惩罚项,以保证控制动作的平滑性。该目标函数可表示为以下数学形式:
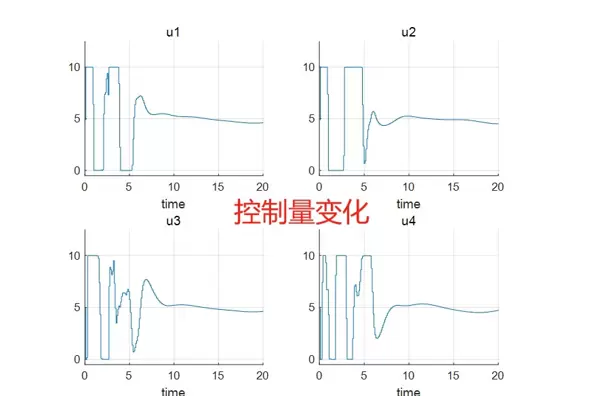
\[ J = \sum_{i=1}^{N_p} (\mathbf{y}_{k+i|k} - \mathbf{r}_{k+i})^T \mathbf{Q} (\mathbf{y}_{k+i|k} - \mathbf{r}_{k+i}) + \sum_{i=0}^{N_c-1} \Delta\mathbf{u}_{k+i|k}^T \mathbf{R} \Delta\mathbf{u}_{k+i|k} \]其中,$\mathbf{y}_{k+i|k}$ 表示在时刻 $k$ 对未来第 $i$ 步的系统输出预测值,$\mathbf{r}_{k+i}$ 为对应的参考轨迹或期望值;$\mathbf{Q}$ 和 $\mathbf{R}$ 分别是输出误差和控制增量的权重矩阵;$\Delta\mathbf{u}_{k+i|k} = \mathbf{u}_{k+i|k} - \mathbf{u}_{k+i-1|k}$ 表示控制量的变化量。
通过求解上述优化问题,可以获得一个最优的控制序列 $\mathbf{U}_{k|k}^*$。但在实际应用中,仅采用该序列中的第一个控制输入 $\mathbf{u}_{k|k}^*$ 作为当前时刻的执行值,随后在下一采样周期重新进行滚动优化。
下面给出一个基于 Python 的线性 MPC 实现示例,使用
cvxpyimport cvxpy as cp
import numpy as np
# 假设已经定义好A, B, Q, R, Np, Nc等参数
# 这里简单给出示例值
A = np.random.rand(12, 12)
B = np.random.rand(12, 4)
Q = np.eye(12)
R = np.eye(4)
Np = 10
Nc = 5
# 定义优化变量
U = cp.Variable((4, Nc))
X = cp.Variable((12, Np + 1))
# 定义约束条件
constraints = [X[:, 0] == x0] # x0是当前状态
for i in range(Np):
if i < Nc:
constraints.append(X[:, i + 1] == A @ X[:, i] + B @ U[:, i])
else:
constraints.append(X[:, i + 1] == A @ X[:, i])
# 定义优化目标
cost = 0
for i in range(Np):
cost += cp.quad_form(X[:, i] - r[i], Q)
for i in range(Nc):
if i > 0:
cost += cp.quad_form(U[:, i] - U[:, i - 1], R)
else:
cost += cp.quad_form(U[:, i], R)
# 求解优化问题
prob = cp.Problem(cp.Minimize(cost), constraints)
prob.solve()
# 获取最优控制输入
u_opt = U[:, 0].value在代码实现过程中,首先定义了两个关键变量:
UXcostcvxpyu_opt非线性MPC在四旋翼系统中的推导
非线性模型预测控制的基本思想与线性MPC一致,但由于系统模型本身具有非线性特性,其优化问题不再属于二次规划范畴,而是转化为一个非线性规划问题(NLP),求解难度显著增加。
此时,系统的预测模型由非线性动力学函数决定,表达式如下:
\[ \mathbf{X}_{k+1|k} = f(\mathbf{X}_{k|k}, \mathbf{U}_{k|k}) \]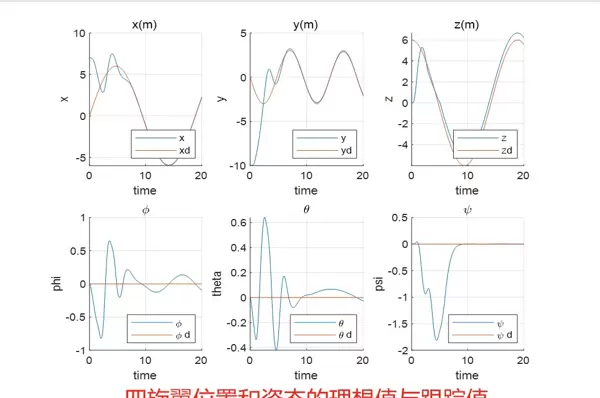
这里的 $f$ 是由四旋翼飞行器的非线性运动方程所确定的映射关系,能够更精确地描述其在三维空间中的姿态与位置演化过程。
尽管模型变得复杂,优化目标的形式仍保持相似,依旧旨在最小化跟踪误差与控制变化的综合代价:
\[ J = \sum_{i=1}^{N_p} (\mathbf{y}_{k+i|k} - \mathbf{r}_{k+i})^T \mathbf{Q} (\mathbf{y}_{k+i|k} - \mathbf{r}_{k+i}) + \sum_{i=0}^{N_c-1} \Delta\mathbf{u}_{k+i|k}^T \mathbf{R} \Delta\mathbf{u}_{k+i|k} \]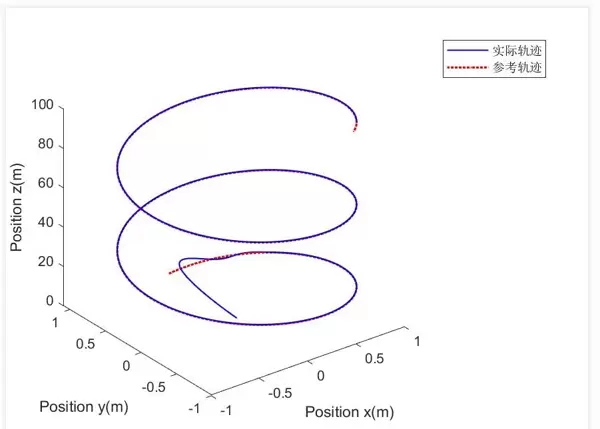
由于目标函数和约束条件可能均为非线性,求解此类 NLP 问题需依赖高效的非线性优化算法,如内点法、序列二次规划(SQP)等。考虑到其实现复杂度较高,且涉及大量数值计算细节,本文暂不提供具体的编程实现示例。
基于线性MPC的四旋翼路径跟踪仿真分析
利用前述设计的线性MPC控制器,可以开展四旋翼飞行器的路径跟踪仿真研究。在实验设置中,预设一条期望轨迹,例如圆形路径或直线路径,运行控制器后观察实际飞行轨迹与目标轨迹之间的吻合程度。
在仿真过程中,可通过调节权重矩阵 $\mathbf{Q}$ 与 $\mathbf{R}$ 来评估其对控制性能的影响:
- 增大 $\mathbf{Q}$ 意味着更加重视轨迹跟踪精度,促使飞行器更紧密地跟随期望路径,但可能导致控制输出频繁大幅调整;
- 而增大 $\mathbf{R}$ 则倾向于抑制控制量的剧烈变动,使操纵更为平稳,但可能会牺牲一定的跟踪精度。
通过对线性与非线性MPC在相同场景下的仿真对比,可以深入理解两者在控制精度、实时性、鲁棒性等方面的差异,从而为实际工程应用中的控制器选型提供理论支持和技术参考。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







