如何进行负二项回归分析？

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

如果研究X对于Y的影响，Y是计数资料，一般可以使用Poisson回归进行研究。但是Poisson回归要求数据满足等离散现象（平均值与方差相等），如果说数据具有一定的聚焦性，此时很可能就会产生过离散现象，即数据平均值与方差明显不相等。此时使用负二项回归更为科学。

比如研究传染病人数，传染病人数明显具有一些空间聚焦现象；以及专利数量，很可能企业之间存在着某种空间意义上的竞争，导致数据具有聚焦现象，诸如此类数据其并不满足Poisson分布的独立性原则。此类数据通常情况下方差会明显的大于平均值，属于过离散数据，此种数据在进行Poisson回归时会导致模型参数估计值的标准误偏小

因而，如果计数资料不适合Poisson分布时，尤其是数据过离散时，此时使用负二项回归分析更合适。

1、案例背景

当前有一项针对专利数量的影响关系研究，研究ZF对于企业的支持力度，是否一线城市，对于企业专利数量的影响情况。共收集10个城市的数据，如下：

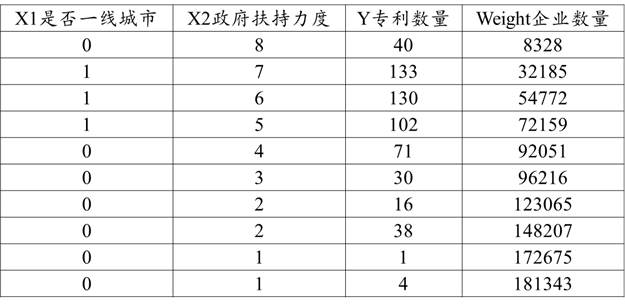
X1是否一线城市：数字1表示为一线城市，数字0表示非一线城市
X2ZF扶持力度：数字越大表示对于企业申请专利时的扶持力度越大
Y专利数量：数字表示某城市调研所有企业申请成功的专利数量
Weight企业数量：数字表示某城市调研的企业数量

2、理论

关于过离散的检验有很多检验方法，在SPSSAU系统中可有三种方式进行综合判断，分别如下：

• 如果说描述分析时发现平均值与方差值有着较大的差异，则说明负二项回归较合理，如果说平均值与方差值基本相等，说明可能使用Poisson回归较为合适。
• 过离散现象可通过O检验（在Poisson回归分析时SPSSAU默认有提供）
• 过离散现象的检验可针对alpha值进行检验，在负二项回归时默认输出，如果alpha值显著不为0（对应的P值小于0.05），则说明使用负二项回归较为合理，反之则说明可能使用Poisson回归较优。

3、操作

登录SPSSAU，选择【实验/医学研究】–【负二项回归】。

本例子中专利数量是基于‘Weight企业数量’，因此‘基数Eposure【可选】’框中应该放入‘Weight企业数量’这项，如下图：

4、SPSSAU结果分析

（1）过度离散检验

在进行负二项回归之前，专利数量的平均值是56.500，方差是2480.944，明显平均值与方差不相等，存在过离散现象。而且使用SPSSAU的Poisson回归时，对其提供的O检验发现，O值明显大于1.96（p=0.000 <0.05），拒绝等离散假定，说明数据存在明显的过离散现象，因此使用负二项回归较为适合。

（2）负二项回归模型似然比检验

SPSSAU共输出两个表格，分别是“负二项回归模型似然比检验”，“负二项回归分析结果汇总”。 “负二项回归模型似然比检验”是针对整个模型的检验，如果说模型p值小于0.05，意味着放入自变量更优，即模型有意义。“负二项回归分析结果汇总”是回归结果的具体结果。

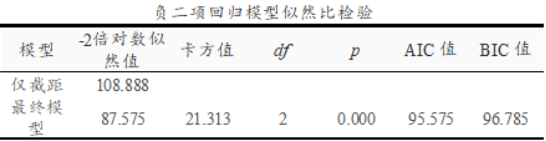
模型似然比检验用于对整体模型有效性进行分析。

第一：首先对p值进行分析，如果该值小于0.05，则说明模型有效；反之则说明模型无效；

第二：AIC值和BIC值可用于多次分析模型时的对比；此两个值越低越好；如果多次进行分析，对比该两个值的变化情况，综合说明模型构建的优化过程；

首先对模型整体有效性进行分析，模型检验的原定假设为：是否放入自变量（X1是否一线城市, X2ZF扶持力度）两种情况时模型质量均一样；检验p值为0.000小于0.05，因而说明拒绝原定假设，即说明本次构建模型时，放入的自变量具有有效性，本次模型构建有意义。

（3）负二项回归分析结果汇总表

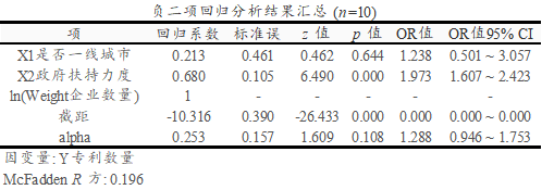
从上表可知，将X1是否一线城市, X2ZF扶持力度共2项为自变量，而将Y专利数量作为因变量进行负二项回归分析，从上表可以看出，模型公式为：Log(Y)=-10.316 + 0.213X1是否一线城市 + 0.680X2ZF扶持力度 + ln(Weight企业数量)。模型的伪R方值（McFadden R 方）为0.196，说明研究模型可以解决专利数量19.6%的原因。具体分析可知：

X1是否一线城市的回归系数值为0.213，但是并没有呈现出显著性(z=0.462，p=0.644>0.05)，意味着X1是否一线城市并不会对Y专利数量产生影响关系，即城市类别与专利数量无明显关系。X2ZF扶持力度的回归系数值为0.680，并且呈现出0.01水平的显著性(z=6.490，p=0.000 <0.01)，意味着X2ZF扶持力度会对Y专利数量产生显著的正向影响关系,以及优势比(OR值, exp(b)值)为1.973，意味着X2ZF扶持力度增加一个单位时，Y专利数量的增加幅度为1.973倍。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏4 回帖

关键词：负二项回归 回归分析 Poisson回归 poisson Weight