对贷款条件实现决策树分类

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

一、背景

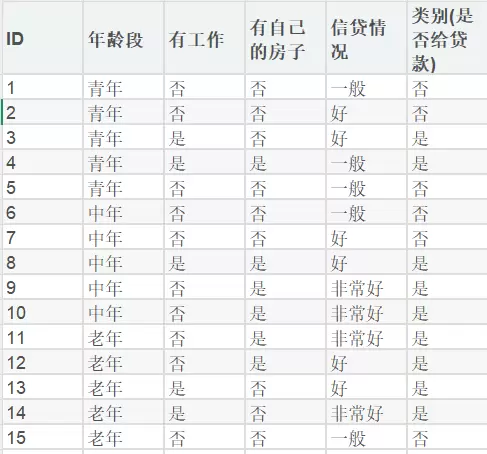
针对贷款申请人的年龄状况、工作状况、房产状况及信贷状况等条件，通过决策树分类法实现，将其归类为是否批准贷款。

二、决策树分类的基本原理与三大算法

2.1 基本原理

决策树分类是一种树状结构的监督学习方法，其核心理念是模仿人类大脑进行决策的过程。

• 树形结构：根节点代表整个数据集，内部节点表示特征判断，叶节点标识预测类别。
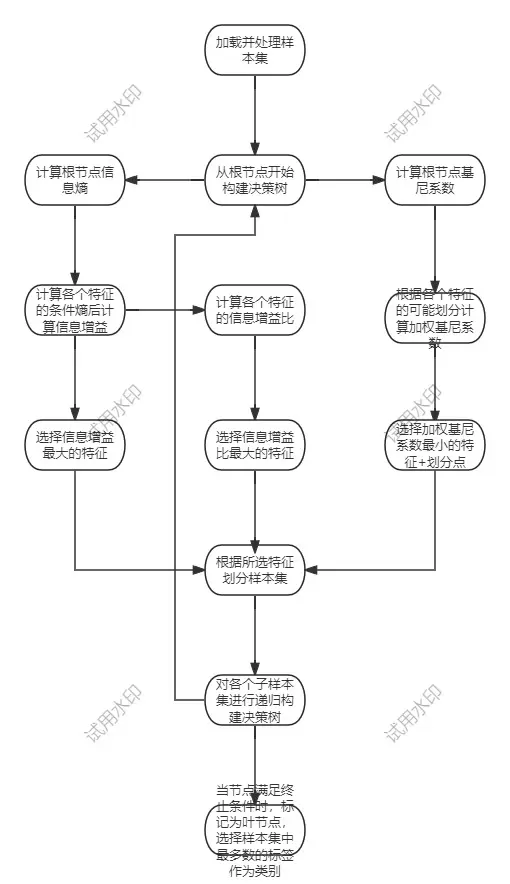
• 主要思路：从根节点出发，根据特征逐步分割数据集，每次分割都使子数据集的纯净度提高，直至叶节点满足停止条件（单一类别/无可用特征划分/样本集合为空）。

衡量纯净度的标准：熵 或 基尼指数，值越小，纯净度越高。

2.2 三大算法

2.2.1 ID3 算法

本质是寻找提升纯净度最多的特征，通过信息增益选择最佳特征，仅适用于分类任务。

1. 初始化：将所有样本作为根节点，并计算根节点的信息熵。

2. 特征筛选：对每个未使用的特征，计算其信息增益。

3. 选择特征：选取信息增益最大的特征作为当前节点的划分标准。
4. 生成子节点：根据该特征的所有可能值，将数据划分为多个子集，每个子集对应一个子节点。
5. 递归终止：如果子节点样本全部属于同一类别（熵=0），或无剩余特征，或子集样本数量过少，则将子节点设为叶节点（类别为子集中最普遍的类）；否则对每个子节点重复步骤2-4。

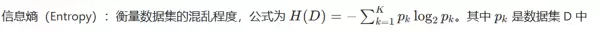
2.2.2 C4.5 算法

ID3 算法倾向于选择取值多的特征，易导致过拟合。C4.5 引入了对特征固有价值惩罚，以抵消其取值多的优势，通过信息增益比选择最佳特征，仅适用于分类任务。

1. 初始化：将所有样本作为根节点，并计算根节点的信息熵。
2. 特征筛选：对每个未使用的特征，计算其信息增益和固有价值，然后计算信息增益比。

3. 选择特征：选取信息增益比最大的特征作为当前节点的划分标准。
4. 生成子节点：根据该特征的所有可能值，将数据划分为多个子集，每个子集对应一个子节点。
5. 递归终止：如果子节点样本全部属于同一类别（熵=0），或无剩余特征，或子集样本数量过少，则将子节点设为叶节点（类别为子集中最普遍的类）；否则对每个子节点重复步骤2-4。

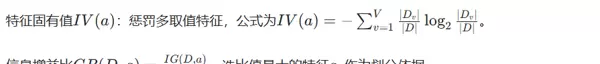
2.2.3 CART 算法

CART（分类与回归树）是目前应用最为广泛的决策树算法，支持分类和回归任务。无论特征是离散的还是连续的，每次划分都将当前数据集分为两部分（二叉结构），并且要找到能够最大化划分后纯净度提升的“特征 + 划分点”组合。

1. 初始化：根节点为全部样本，计算根节点的基尼指数。

2. 特征筛选：对每个特征，遍历其所有可能的划分方式（离散特征：每个值对应“是/否”拆分；连续特征：每个候选点对应“≤/>”拆分）；对每种划分方式，计算划分后的加权基尼指数。

3. 选择最佳划分：选取加权基尼指数最小的“特征 + 划分点”，生成两个子节点。
4. 递归终止：如果子节点样本全部属于同一类别、无剩余特征或样本数量过少，则设为叶节点；否则重复步骤2-3。

三、决策树分类实现

3.1 收集数据

已有训练数据集dataset.txt和测试数据集testset.txt。

• dataset.txt：构建决策树模型。
• testset.txt：评估模型精度。

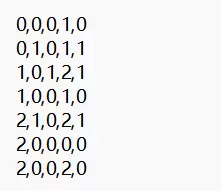
3.2 分析处理数据

特征标签与数字化对应关系如下：

1. 特征：

   0: {'年龄段': '青年', '有工作': '否', '有自己的房子': '否', '信贷情况': '一般'},
   1: {'年龄段': '中年', '有工作': '是', '有自己的房子': '是', '信贷情况': '好'},
   2: {'年龄段': '老年', '有工作': '是', '有自己的房子': '是', '信贷情况': '非常好'}
               

2. 标签：

   0：是（给贷款）；
   1：否（不给贷款）；
               

3.3 训练模型

分别使用三种算法构建决策树模型，并将其可视化。

3.4 测试模型

通过测试训练集计算三种决策树模型的分类准确度。

四、具体代码实现

4.1 配置与依赖引入

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import FancyBboxPatch, FancyArrowPatch

# --- 中文显示配置 ---
plt.rcParams["font.family"] = ["SimHei", "Microsoft YaHei"]
plt.rcParams["axes.unicode_minus"] = False
plt.rcParams["font.size"] = 10

导入数值计算库

numpy

和

绘图库

matplotlib；

配置以支持中文显示和正确显示负号，确保可视化结果美观。

matplotlib

4.2 数据加载与核心工具函数

def load_data(file_path):
    """加载数据集"""
    try:
        return np.loadtxt(file_path, delimiter=',', dtype=int)
    except FileNotFoundError:
        print(f"错误：文件 '{file_path}' 未找到。")
        return None


def get_feature_meta():
    """特征名称与取值映射"""
    feature_names = ['年龄段', '有工作', '有自己的房子', '信贷情况']
    value_map = {
        0: {'年龄段': '青年', '有工作': '否', '有自己的房子': '否', '信贷情况': '一般'},
        1: {'年龄段': '中年', '有工作': '是', '有自己的房子': '是', '信贷情况': '好'},
        2: {'年龄段': '老年', '有工作': '是', '有自己的房子': '是', '信贷情况': '非常好'}
    }
    return feature_names, value_map


def entropy(labels):
    """计算信息熵"""
    p = np.bincount(labels) / len(labels)
    return -np.sum(p * np.log2(p, out=np.zeros_like(p), where=(p > 0)))


def gini(labels):
    """计算Gini系数"""
    p = np.bincount(labels) / len(labels)
    return 1 - np.sum(p ** 2)


def majority_vote(labels):
    """多数投票"""
    return np.argmax(np.bincount(labels))

数据加载：

load_data

和

get_feature_meta

负责数据的输入和解析。

数学基础：

entropy

和

gini

是决策树特征选择的核心指标。

辅助决策：

majority_vote

用于在无法继续划分时，确定叶节点的类别。

4.3 决策树节点结构

# --- 决策树节点类 ---
class TreeNode:
    __slots__ = ['feat_idx', 'feat_name', 'val', 'is_leaf', 'label', 'children']

    def __init__(self, feat_idx=None, feat_name=None, val=None, is_leaf=False, label=None, children=None):
        self.feat_idx = feat_idx
        self.feat_name = feat_name
        self.val = val
        self.is_leaf = is_leaf
        self.label = label
        self.children = children or []

定义了决策树的基本构成单元

TreeNode

每个节点包含：

• 用于划分的特征索引和名称（

  feat_idx

  ，

  feat_name

  ）。
• 到达该节点的特征值（

  val

  ）。
• 是否为叶节点（

  is_leaf

  ），如果是，则包含类别标签（

  label

  ）。
• 子节点列表（

  children

  ）。

4.4 决策树构建算法（核心）

# --- 决策树构建算法 ---
def build_tree(data, feat_names, algorithm='ID3', print_metrics=True):
    """
    统一的树构建入口
    algorithm: 'ID3', 'C4.5', 'CART'
    """
    labels = data[:, -1]
    feat_indices = list(range(data.shape[1] - 1))

    def _build(current_data, current_feats, depth=0):
        current_labels = current_data[:, -1]

        # 1. 如果所有样本属于同一类别，返回叶节点
        if len(np.unique(current_labels)) == 1:
            return TreeNode(is_leaf=True, label=int(current_labels[0]))

        # 2. 如果没有特征可分或样本数为0，返回多数投票结果
        if len(current_feats) == 0 or current_data.size == 0:
            return TreeNode(is_leaf=True, label=majority_vote(labels))

        best_idx = -1
        best_metric = -np.inf if algorithm != 'CART' else np.inf

        # 打印当前节点的计算信息
        if print_metrics and depth == 0:
            print(f"\n===== {algorithm} 特征选择指标 =====")
            header = f"{'特征':<8} {'熵':<8} {'增益':<8}" if algorithm != 'CART' else f"{'特征':<8} {'Gini':<8}"
            if algorithm == 'C4.5': header += f" {'增益比':<8}"
            print(header)
            print("-" * 32)

        # 3. 选择最优特征
        for idx in current_feats:
            feat_name = feat_names[idx]
            values = current_data[:, idx]

            if algorithm in ['ID3', 'C4.5']:
                ent = entropy(current_labels)
                cond_ent = 0.0
                split_info = 0.0
                for v in np.unique(values):
                    subset = current_data[values == v]
                    p = len(subset) / len(current_data)
                    cond_ent += p * entropy(subset[:, -1])
                    split_info -= p * np.log2(p) if p > 0 else 0

                gain = ent - cond_ent
                metric = gain if algorithm == 'ID3' else gain / (split_info + 1e-10)

                if print_metrics and depth == 0:
                    print(f"{feat_name:<8} {ent:.4f} {gain:.4f}" + (f" {metric:.4f}" if algorithm == 'C4.5' else ""))
            else:  # CART
                weighted_gini = 0.0
                for v in np.unique(values):
                    subset = current_data[values == v]
                    weighted_gini += (len(subset) / len(current_data)) * gini(subset[:, -1])
                metric = weighted_gini
                if print_metrics and depth == 0:
                    print(f"{feat_name:<8} {metric:.4f}")

            # 更新最优特征
            if (algorithm != 'CART' and metric > best_metric) or (algorithm == 'CART' and metric < best_metric):
                best_metric = metric
                best_idx = idx

        best_name = feat_names[best_idx]
        if print_metrics:
            print(f"-> 选择特征: '{best_name}' (最优{algorithm}指标: {best_metric:.4f})")

        # 4. 递归构建子树
        node = TreeNode(feat_idx=best_idx, feat_name=best_name)
        remaining_feats = [f for f in current_feats if f != best_idx]

        for val in np.unique(current_data[:, best_idx]):
            child_node = _build(current_data[current_data[:, best_idx] == val], remaining_feats, depth + 1)
            child_node.val = val
            node.children.append(child_node)

        return node

    return _build(data, feat_indices)

通过一个嵌套的递归函数（

_build

）来构造树。
终止条件：检查是否所有样本属于同一类别，或没有特征可选，或样本数过少。如果是，则返回叶节点。
特征选择：
ID3：计算每个特征的信息增益，选取增益最大的特征。
C4.5：计算每个特征的信息增益比，选取增益比最大的特征。
CART：计算每个特征的加权基尼系数，选取系数最小的特征。
树的生长：根据最优特征的不同取值，将数据分割成子集，并为每个子集递归调用（

_build

）函数，生成子节点。

4.5 预测与模型评估

# --- 预测与评估 ---
def predict(node, sample):
    """预测单个样本"""
    current = node
    while not current.is_leaf:
        feat_val = sample[current.feat_idx]
        try:
            current = next(child for child in current.children if child.val == feat_val)
        except StopIteration:
            return 0  # 遇到未见过的特征值，返回默认值
    return current.label


def accuracy(tree, test_data):
    """计算准确率"""
    if test_data is None or test_data.size == 0: return 0
    predictions = [predict(tree, sample[:-1]) for sample in test_data]
    return np.mean(predictions == test_data[:, -1])

预测：

predict

函数从根节点开始，根据输入样本的特征值，沿着树的分支向下遍历，直到到达一个叶节点，返回该叶节点的类别作为预测结果。
评估：

accuracy

函数使用

predict

函数对测试集中的所有样本进行预测，然后将预测结果与实际标签进行对比，计算预测正确的比例，即准确率。

4.6 决策树可视化

# --- 可视化 (精简版) ---
def visualize_tree(tree, title, value_map):
    """可视化决策树"""

    def get_layout(node, depth=0, pos_x=0.5):
        y = 0.9 - depth * 0.3
        info = {'x': pos_x, 'y': y, 'node': node, 'children': []}
        if not node.is_leaf:
            num_children = len(node.children)
            if num_children > 1:
                width = min(0.8, num_children * 0.25)
                child_xs = np.linspace(pos_x - width / 2, pos_x + width / 2, num_children)
            else:
                child_xs = [pos_x]
            for i, (child, cx) in enumerate(zip(node.children, child_xs)):
                info['children'].append(get_layout(child, depth + 1, cx))
        return info

    def plot_node(info, ax):
        x, y = info['x'], info['y']
        node = info['node']
        if node.is_leaf:
            color = (0.7, 0.95, 0.7) if node.label == 1 else (0.95, 0.7, 0.7)
            edge_color = (0.2, 0.6, 0.2) if node.label == 1 else (0.6, 0.2, 0.2)
            text = "给贷款" if node.label == 1 else "不给贷款"
            bbox = FancyBboxPatch((x - 0.08, y - 0.04), 0.16, 0.08, boxstyle="round,pad=0.01", facecolor=color,
                                  edgecolor=edge_color)
        else:
            bbox = FancyBboxPatch((x - 0.1, y - 0.04), 0.2, 0.08, boxstyle="round,pad=0.01",
                                  facecolor=(0.7, 0.85, 0.95), edgecolor=(0.2, 0.4, 0.6))
            text = f"{node.feat_name}?"

        ax.add_patch(bbox)
        ax.text(x, y, text, ha='center', va='center', fontsize=9)

        for child_info in info['children']:
            ax.annotate('', xy=(child_info['x'], child_info['y'] + 0.04), xytext=(x, y - 0.04),
                        arrowprops=dict(arrowstyle='->', lw=1, color='gray'))
            label_text = value_map[child_info['node'].val][node.feat_name]
            ax.text((x + child_info['x']) / 2, (y - 0.04 + child_info['y'] + 0.04) / 2,
                    label_text, ha='center', va='center', fontsize=8,
                    bbox=dict(boxstyle="round,pad=0.01", fc="white", alpha=0.8))
            plot_node(child_info, ax)

    fig, ax = plt.subplots(figsize=(10, 6))
    ax.set_xlim(-0.1, 1.1)
    ax.set_ylim(-0.1, 1.0)
    ax.axis('off')
    plot_node(get_layout(tree), ax)
    plt.title(title, fontsize=14)
    plt.tight_layout()
    plt.show()

以图形化方式展示抽象的决策树结构，便于直观理解。
通过递归计算节点位置（

get_layout

）和绘制节点与连线（

plot_node

），生成一棵自上而下的决策树图。
叶节点会根据类别（给贷款 / 不给贷款）显示不同的颜色。

4.7 主函数与流程控制

# --- 主函数 ---
def main():
    train_file = "C:/Users/zheng/Desktop/dataset.txt"
    test_file = "C:/Users/zheng/Desktop/testset.txt"

    train_data = load_data(train_file)
    test_data = load_data(test_file)

    if train_data is None:
        return

    feat_names, value_map = get_feature_meta()

    for algo in ['ID3', 'C4.5', 'CART']:
        print(f"\n{'=' * 20} 构建 {algo} 决策树 {'=' * 20}")
        tree = build_tree(train_data, feat_names, algorithm=algo)
        acc = accuracy(tree, test_data)
        print(f"\n{algo} 决策树在测试集上的准确率: {acc:.2%}")
        visualize_tree(tree, f"{algo} 决策树", value_map)


if __name__ == "__main__":
    main()

定义了程序的执行流程：
1. 加载训练和测试数据。
2. 依次使用 ID3, C4.5, CART 三种算法构建决策树。
3. 对每种算法构建的树，计算其在测试集上的准确率。
4. 可视化已构建好的决策树。

五、总结
本次决策树分类实验以贷款审批场景为目标，通过模块化代码完整实现了 ID3、C4.5、CART 三种算法，关键在于明确各算法特征选择逻辑（ID3 使用信息增益、C4.5 使用信息增益比、CART 使用加权基尼系数）。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：贷款条件 决策树 Matplotlib Algorithm delimiter