摘要
本文展示了迭代卡尔曼滤波(IKF)更新作为高斯-牛顿方法在近似最大似然估计(MLE)中的应用。此外,提供了一个实例,展示了在观测精度提升时,迭代卡尔曼滤波更新和最大似然估计表现出正确的收敛特性,而扩展卡尔曼滤波(EKF)更新则不具备此特性。
引言
针对离散时间动力系统的状态估计问题,基本的滤波解决方案可以概括为由“预测”和“更新”两个阶段组成的递归过程。特别是对于卡尔曼滤波器(Kalman Filter)、扩展卡尔曼滤波器(EKF)和迭代卡尔曼滤波器(IKF),这一过程同样适用。这些变体主要用于处理非线性测量函数的问题。
在仅进行一次迭代的情况下,IKF的更新方法会退化为EKF的更新方法;当测量函数为仿射时,这两种方法又会退化为标准的卡尔曼更新。虽然IKF需要更多的计算资源,但其性能通常优于EKF。关于这些滤波器的详细讨论,可参考文献[3]、[41]和[6]。
我们应用最大似然/最小二乘方法解决(非线性)更新问题,并证明IKF的更新方法实际上是在使用高斯-牛顿方法寻找近似解。这使得我们可以将文献[3]中对IKF的处理与文献[1]中对改进牛顿方法的处理结合起来。
我们还提供了一个双基地测距问题的例子,其中IKF和最大似然解都可以通过代数形式的闭式解表示。在这个例子中,当观测变得更加准确时,最大似然解和IKF解都能正确收敛。然而,EKF的更新则会收敛到一个有偏值,并且其误差协方差会收敛至零。这种“错误收敛”的情况在更广泛的情境下也成立,即当精确测量能完全确定系统状态时,对于具有足够维度的非线性测量函数,会出现类似的现象。
更新问题
动力系统的更新问题与静态估计问题等价,即根据当前的观测值来修正当前(预测的)状态估计。在这个问题中,系统的动态模型不起作用。
我们采用以下符号和约定:状态空间和测量空间分别是维度为\( n \)和\( m \)的实向量空间。设\( x \in \mathbb{R}^n \)表示当前的真实状态,\( \hat{x} \)表示当前的状态估计,\( z \in \mathbb{R}^m \)表示观测量。测量函数\( h: \mathbb{R}^n \rightarrow \mathbb{R}^m \)(其中\( h(x) \)表示无噪声的测量值)是二次可微的,其一阶导数记为\( h' \)。
在本文中,\( \delta x \in \mathbb{R}^n \)表示自由变量向量。所有向量均视为列向量,即列维度为1的矩阵。矩阵\( M \)的转置记为\( M^* \)。
我们将\( z \)和\( \hat{x} \)视为相互独立的随机向量的实现,它们具有多元正态分布:
\[ z \sim \mathcal{N}(h(x), R), \qquad \hat{x} \sim \mathcal{N}(x, P). \]其中\( z, \hat{x}, R, P \)的取值已知。更新问题的目标是利用当前信息求得更优的状态估计\( \hat{x}^+ \)及其对应的协方差\( P^+ \)。
IKF与EKF的更新方法
这里简要回顾迭代卡尔曼滤波(IKF)和扩展卡尔曼滤波(EKF)中使用的更新公式。对于任意自然数\( i \),IKF给出如下更新:
状态更新:\( \hat{x}^+ = x_i \)
协方差更新:\( P^+ = P_i \)
序列\( \{x_i\} \)和\( \{P_i\} \)按以下方式递归定义:
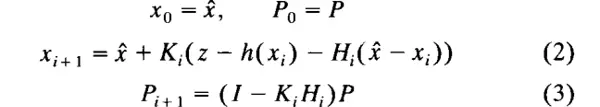
其中
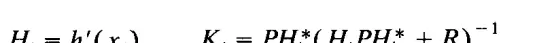
对于单次迭代,在上述公式(2)与(3)中取\( i = 0 \),即可得到EKF(扩展卡尔曼滤波)的更新公式。
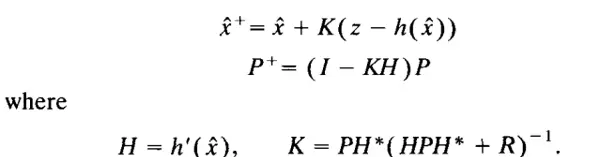
最大似然更新
为了便于说明,我们将当前观测与当前状态估计合并成一个单一的“观测”向量。因此,我们构建扩展(增广)的观测向量与测量函数:
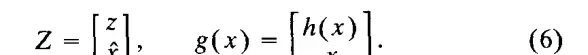
从式(1)及独立性假设出发,可以重新阐述更新问题如下:给定 Z、Q 和 g,目标是计算状态估计 x 及其对应的协方差 P。
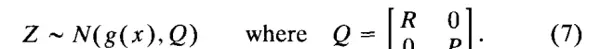
回忆一下,似然函数 L(δ) 是将 x 替换为自由变量 δ 后 Z 的概率密度函数。最大似然估计及其协方差的近似值由以下公式给出:
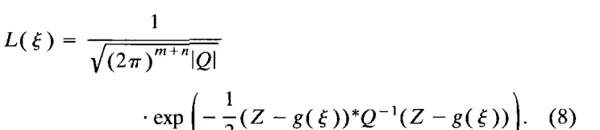
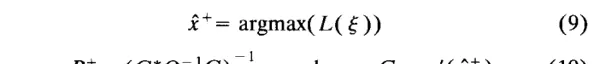
由于最大化 L(θ) 等同于最小化其对数值的相反数,因此公式(9)可以等效地表示为:
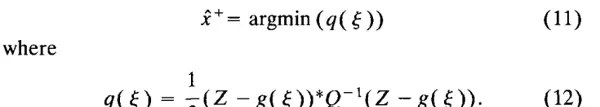
求极值所需的微分条件 q'(θ) = 0 被称为 x 的最大似然方程。对于当前情况,该方程表示为:
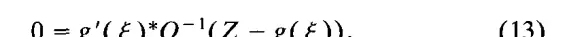
接下来的两个部分将讨论高斯-牛顿技术用于近似 f + f 的方法,以及它与 IKF 更新方法的等价性。这里首先推导公式(10),并解释其与 IKF 协方差方程的关系 [见(3)]。
对 X - x 协方差的近似基于这样的假设:给定的 X 实现足够接近 x,允许将 g 替换为其一阶近似。即假设 g 在 x 和 x 的邻域内是仿射的。因此有 g(ξ) = g(x*) + G(ξ - x),其中 G = g'(ξ) = g'(x) 为常数。设 V = Z - g(x),根据公式(7)可知 V ~ N(0, Q)。将 ξ 代入公式(13)中,我们得到:
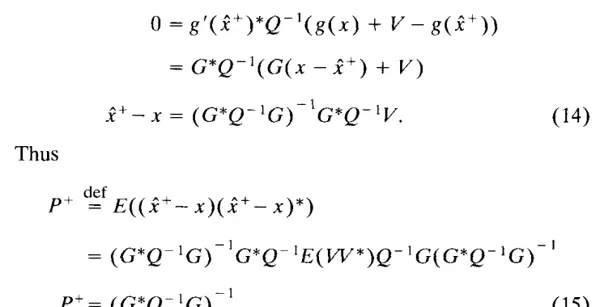
该表达式与涉及卡尔曼增益的公式相关联。因为:
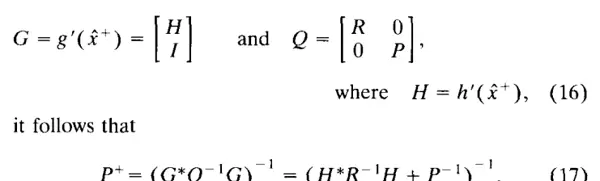
矩阵求逆引理指出,对于任意可逆矩阵 R 和 P,以及任何维度匹配的矩阵 H,矩阵求逆引理都成立。这可以通过在左侧乘以 HRH + P,在右侧乘以 HPH + R 来验证。由公式(17)和(18)得出:
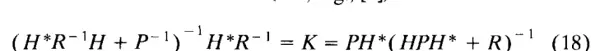
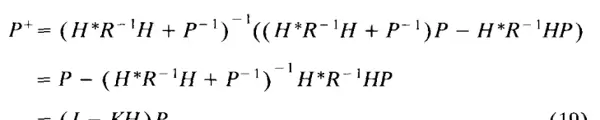
这是以卡尔曼增益表示的协方差更新公式的常见形式。
5. 高斯-牛顿方法
采用文献 [2, 定义 10.1.1] 的符号,非线性最小二乘问题可以表示为:
minimize f(ξ) = |r(ξ)| (20)
其中 r: R → R 是二阶可微函数,|y| = √(y*y) 是 y ∈ R 上的常规范数。
解决这个问题的高斯-牛顿方法是将近似牛顿法应用于寻找梯度函数零点的问题,即 f'(ξ) = r'(ξ)*r(ξ)(这里 f: R → R 由 f' 的转置给出)。
回顾牛顿法,它是通过构建一个逼近序列 x 来定义解法的:给定初始逼近 x,通过归纳定义后续迭代。
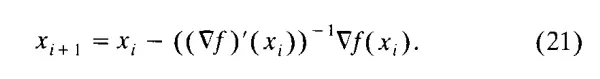
如果 f 是二次的,即 r(等价于 f)是仿射的,那么 x 可以在一步中解决问题。通常情况下,如果 lim(i→∞) x = c 存在,并且 (f)'(c) 可逆,那么 f(c) = 0,表明 c 是 f 的一个临界点。
设 H 为 r 的第 j 个分量的 Hessian 矩阵,则有 (f)'(ξ) = r'(ξ)*r'(ξ) + D(ξ), D(ξ) = Σ r(ξ)H(ξ)。高斯-牛顿方法忽略了公式中的 D 项,从而得到逼近序列:
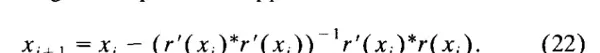
需要注意的是,如果 r 是仿射的,那么 D = 0,可以看到高斯-牛顿方法的操作方式是通过连续最小化来进行的。
更新规则 \(x_{i+1} = \arg\min | f(\xi; x_i) |^2\),其中 \(f(\xi; x_i) = r(x_i) + r'(x_i)(\xi - x_i)\) 是 \(r\) 在 \(x_i\) 点的仿射近似。有关高斯-牛顿方法收敛速率的详细说明,请参见 [2, 定理 10.2.1]。
6. IKF 更新是一种高斯-牛顿方法
利用前几节的符号,设 \(S\) 是 \(Q^{-1}\) 的“平方根”(即满足 \(S^*S = Q^{-1}\)),并定义函数 \(r(\xi) = S(Z - g(\xi))\),其中 \(r: \mathbb{R}^n \to \mathbb{R}^m\)。注意,最大似然问题 (12) 的目标函数与非线性最小二乘问题 (20) 的目标函数相同。
我们使用替代方程 (24) 来评估 (22) 的高斯-牛顿迭代。注意到 \(r'(\xi) = -S g'(\xi)\)。
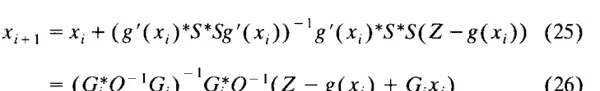
其中 \(G_i = g'(x_i)\)。利用公式 (6)、(16)、(17) 以及矩阵求逆引理 (18),我们得到:
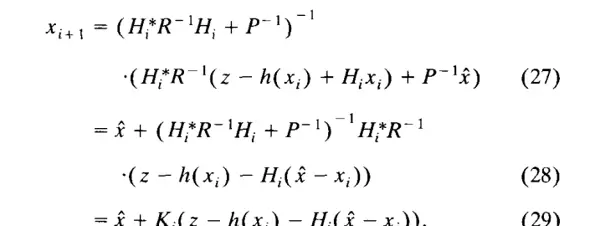
通过数学归纳法可以得出:使用初始估计 \(\hat{x}\) 的高斯-牛顿方法生成的迭代序列,与 IKF(迭代卡尔曼滤波)生成的迭代序列是完全相同的。
7. 示例说明
在本节中,我们给出一个二维双基地测距(bistatic ranging)示例,其中最大似然(maximum likelihood)、EKF 和 IKF 的解均可用代数表达式表示。该示例展示了:随着观测变得更精确,最大似然和 IKF 的解能够正确收敛。而 EKF 的更新解则显示出,即便其误差协方差趋近于零,结果仍会收敛到一个有偏的值。
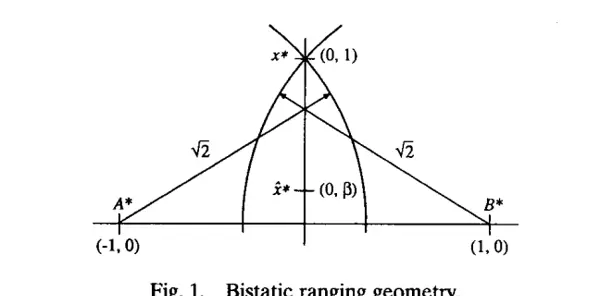
问题的几何示意如图 1 所示。我们有两个测距站,分别位于位置 \(A^* = (-1, 0)\) 和 \(B^* = (+1, 0)\),以及一个当前位于 \(x\) 的被跟踪物体,还有一个当前对物体位置的估计 \(\hat{x}\)。为简化起见,我们假设观测数据由每个测距站测得的半径平方构成。这样可以使测量函数的导数尽可能简单,同时又不是常数。因此,测量函数 \(h: \mathbb{R}^2 \to \mathbb{R}^2\) 及其导数为:
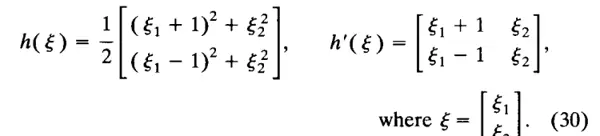
当前物体状态、状态估计以及当前测量值分别为:
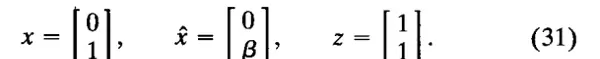
我们假设 \(\hat{x}\) 与 \(z\) 相互独立,并且它们的协方差矩阵为:
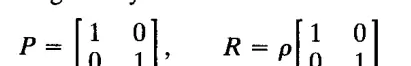
其中 \(P > 0\)。观测 \(z\) 表示一次“近乎完美”的测量,因此 \(p\) 可以取任意小的值。协方差 \(P\) 与当前估计 \(\hat{x}\) 一致,只要 \(|\beta - 1|\) 不太大。注意,测量方程 \(z = h(\xi)\) 有两个解,即 \(x\) 和 \(-x\)。我们假设估计 \(\hat{\xi}\) 更接近 \(x\),即假设 \(\beta > 0\)。
IKF 更新由公式 (2) 和 (3) 给出,利用公式 (17) 和矩阵求逆引理 (18) 可重写为:
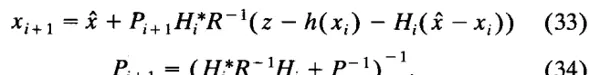
这些表达式可简化为如下形式:
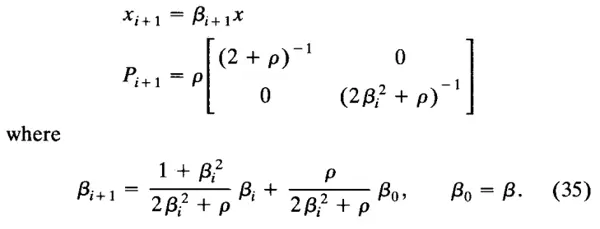
我们通过归纳法在假设 \(x_i = P_i x\) 的基础上进行证明:
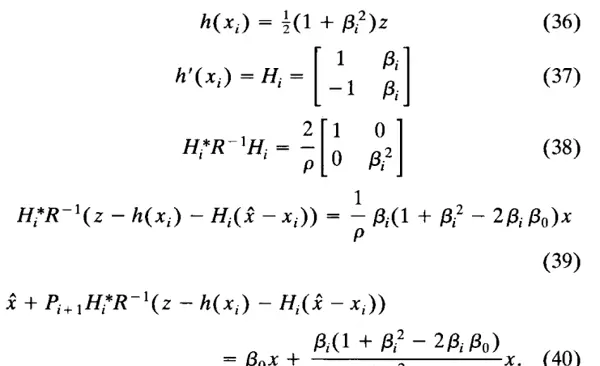
由此可得 \(x_{i+1} = \beta_{i+1}\),完成了归纳证明。令 \(p \to 0\),我们得到:
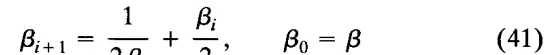
这是著名的 Newton 方法近似序列 \(v_i\)。对于任意 \(\beta > 0\),该序列收敛到 1,从而说明当观测变得更加精确时,IKF/高斯-牛顿方法是收敛的。
另一方面,由于 EKF 更新是 IKF 的第一次迭代,且 \(\beta_0 = \beta\),因此可得:
因此,如果 \(\beta \neq 1\),EKF 更新会收敛到一个有偏值,尽管其误差协方差会收敛到零。
最后,考虑最大似然更新方程 (10) 和 (11)。这些方程的形式为:
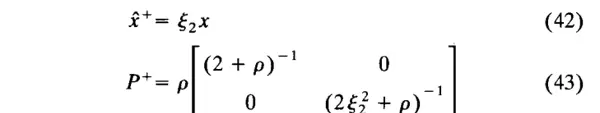
其中 \(A\) 是三次多项式的最大根。
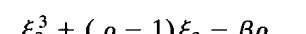
多项式的推导直接来源于 \(P^+\) 是最大似然方程 (13) 的解这一事实。
可以通过公式 (17) 来执行计算。
需要注意的是,当 p 趋向于 0 时,三次多项式的最大根接近 1。这一现象表明,最大似然估计是收敛的,并且其结果与初始协方差矩阵 P 无关。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







