在机器人技术不断发展的今天,六自由度机械臂因其出色的灵活性和广泛的应用前景,被普遍应用于工业自动化、医疗辅助、科研实验等多个领域。为了实现对其运动的高精度控制,模型预测控制(MPC)成为一种高效且先进的控制策略。
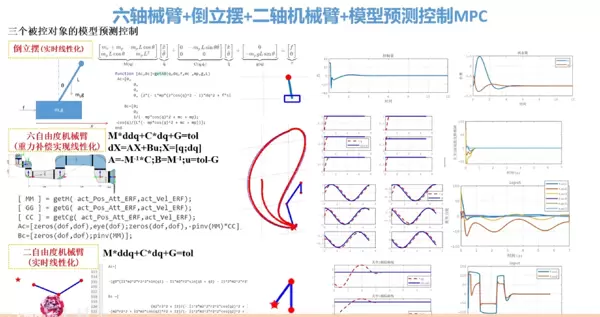
六自由度机械臂的基本特性
这类机械臂通常包含六个独立的关节,每个关节对应一个自由度,使得末端执行器能够在三维空间中完成复杂的空间定位与姿态调整。其运动方式类似于人手臂,支持伸缩、扭转、俯仰等多种动作组合,具备高度的机动性与操作自由度。
模型预测控制(MPC)的核心机制
MPC是一种基于系统动态模型的先进控制方法,其核心在于利用当前状态和系统模型对未来一段时间内的行为进行预测,并在此基础上优化未来的控制输入序列。通过最小化预设的目标函数,使系统的输出尽可能逼近期望轨迹,同时满足各类约束条件。
换句话说,MPC会“提前模拟”系统接下来的行为,并计算出一组最优控制指令,确保系统平稳、准确地达到目标状态。
代码实现与关键步骤分析
1. 建立机械臂的运动学模型
在Python环境中,可以借助相关库来构建机械臂的正向运动学模型,用于从关节角度推导末端执行器的空间位姿。
sympy以下示例展示了如何基于Denavit-Hartenberg(DH)参数和齐次变换矩阵计算机械臂的正向运动学:
from sympy import symbols, sin, cos, Matrix
# 定义关节角度符号
theta1, theta2, theta3, theta4, theta5, theta6 = symbols('theta1 theta2 theta3 theta4 theta5 theta6')
# 定义DH参数
a1, a2, a3, a4, a5, a6 = symbols('a1 a2 a3 a4 a5 a6')
d1, d2, d3, d4, d5, d6 = symbols('d1 d2 d3 d4 d5 d6')
# 建立齐次变换矩阵
T1 = Matrix([[cos(theta1), -sin(theta1), 0, a1 * cos(theta1)],
[sin(theta1), cos(theta1), 0, a1 * sin(theta1)],
[0, 0, 1, d1],
[0, 0, 0, 1]])
T2 = Matrix([[cos(theta2), -sin(theta2), 0, a2 * cos(theta2)],
[sin(theta2), cos(theta2), 0, a2 * sin(theta2)],
[0, 0, 1, d2],
[0, 0, 0, 1]])
# 以此类推,建立其他关节的齐次变换矩阵
# 末端执行器的位姿矩阵
T_end = T1 * T2 * T3 * T4 * T5 * T6通过定义各关节的角度变量及对应的DH参数,逐级构建每个连杆的坐标变换矩阵。将这些矩阵依次相乘,最终获得末端执行器相对于基座的完整位姿信息,包括位置坐标与旋转姿态。
2. MPC控制器的设计与实现
本例以线性二次型调节器(LQR)思想为基础,扩展为有限时域内的模型预测控制器。假设机械臂的动力学模型已被离散化处理,并定义了相应的状态变量与控制输入变量:
xuimport numpy as np
# 假设已经定义好的离散化状态转移矩阵A和控制输入矩阵B
A = np.array([[1.01, 0.1], [0, 0.99]])
B = np.array([[0.01], [0.05]])
# 定义成本函数权重矩阵Q和R
Q = np.diag([1, 1])
R = np.diag([0.1])
# 定义预测时域N
N = 10
# 初始化控制输入序列u
u_sequence = np.zeros((N, 1))
# 迭代求解最优控制输入
for k in range(N - 1):
x_k = np.array([[1], [2]]) # 当前状态,这里假设一个初始值
F = np.zeros((2 * N, 2 * N))
for i in range(N - k - 1):
A_i = np.linalg.matrix_power(A, i + 1)
F[2 * i:2 * (i + 1), 0:2] = A_i
H = R + B.T @ F.T @ Q @ F @ B
f = 2 * B.T @ F.T @ Q @ F @ A @ x_k
u_k = -np.linalg.inv(H) @ f
u_sequence[k] = u_k[0]上述代码段中,首先设定离散化的系统状态转移矩阵
A以及控制输入矩阵
B这两个矩阵共同描述了系统在离散时间步长下的动态演化规律。随后引入成本函数中的权重矩阵
Q和
R其中,
Q用于抑制状态偏差,即让系统状态尽可能接近目标值;而
R则限制控制量的幅度过大,避免执行机构过载或产生剧烈动作。
在设定的预测时域
N内,通过求解一个二次规划问题,得到未来一系列最优控制输入
u_sequence仅实施第一项控制指令,并在下一时刻重新进行滚动优化,从而实现闭环反馈控制。
总结
针对六自由度机械臂的模型预测控制,是一项融合了动力学建模、优化算法与实时控制的综合性技术。通过精确建立机械臂的运动学与动力学模型,并结合MPC的滚动优化机制,能够显著提升控制精度与系统响应性能。
尽管实际应用中还需应对模型不确定性、外部扰动等因素的影响,但MPC提供了一个结构清晰、适应性强的控制框架。本文所展示的原理说明与代码实现,旨在帮助读者理解该方法的基本流程与关键技术点,为进一步深入研究和工程实践打下基础。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







