理解辗转相除法:从迭代到最大公约数的实现
你是否曾对教材中频繁出现的“辗转相除法”感到困惑?为什么非要用这种方法求最大公约数?为什么每次都要判断两个数的大小,甚至进行值的交换?这些问题其实都指向同一个核心——算法设计中的逻辑优化与通用性保障。
接下来我们将一步步解析其原理,并探讨如何通过迭代思想简化代码结构。欢迎在评论区交流你的看法,共同优化实现逻辑。
Fibonacci Series: 0 1 1 2 3 5 8 13 21 34什么是迭代法?
辗转法,也称迭代法,是指利用旧变量的值不断推导出新值的过程。光这么说可能有点抽象,就像听老奶奶讲“dog叫”一样摸不着头脑。我们来看一个典型例子:斐波那契数列。
虽然没学过也没关系,这里只是借用它来说明迭代的思想。观察斐波那契数列:
1, 1, 2;1, 2, 3;2, 3, 5……
从第三项开始,每一项都是前两项之和。设 x1 = 1,x2 = 1,则下一项 X = x1 + x2 = 2。接着更新变量:
x1 = x2;x2 = X;再计算新的 X = x1 + x2
如此循环往复,就能持续生成后续项。这个不断用旧值推出新值的过程,就是迭代的核心所在。

最大公约数的本质
最大公约数(GCD,Greatest Common Divisor)指的是两个或多个整数共有约数中最大的那个。换句话说,它是能同时整除这些数的最大正整数。
举个例子:18 和 21 的最大公约数是 3,而 25 和 15 的是 5。
观察可知,这两个数分别除以它们的最大公约数时,余数为 0。这一点非常重要,将成为后续循环终止的关键条件。

辗转相除法的原理
该方法基于这样一个数学规律:两个整数的最大公约数等于其中较小数和两数相除余数的最大公约数。
具体操作是:用较大数除以较小数,再用余数继续去除较小数,直到余数为 0。此时的除数即为最大公约数。
为了确保每一步都能正确执行,必须保证被除数不小于除数。因此,在每次运算前需判断 m 和 n 的大小关系。
但由于输入顺序不确定,无法预知哪个更大,于是采用一种简单粗暴但有效的方法:若 m < n,则交换二者位置。
这种处理方式虽显“野蛮”,却极大增强了代码的鲁棒性。如果你有更优雅的方案,欢迎提出讨论!

变量交换的艺术:“空杯法”详解
要实现两个变量的值互换,仅靠两者本身无法完成,必须借助第三个临时变量 temp,就像三个杯子倒水一样。
假设 a 杯有 5 口水,b 杯有 10 口水,c 杯为空:
- 先把 a 的水倒入 c(temp = a),a 变空;
- 再把 b 的水倒入 a(a = b),b 变空;
- 最后把 c 的水倒入 b(b = temp),完成交换。
这段看似简单的操作,实则是编程中极为基础且重要的技巧,属于每个开发者都应掌握的“基本功”。
从更高层面看,这其实就是一种解决问题的策略——算法。
int a = 5, b = 10, temp;
temp = a;
a = b;
b = temp;对应代码如下:
if (m < n) {
temp = n;
n = m;
m = temp;
}
这一段实现了数值的强制顺序调整,确保 m ≥ n,为后续迭代做好准备。
核心迭代过程解析
回到辗转相除法的关键部分——循环迭代。还记得前面提到的迭代思想吗?即使暂时遗忘也无妨,重点在于理解以下流程:

将求 GCD 的功能封装成独立函数,不仅使 main 函数简洁清晰,也提高了代码的可读性和复用性。
特别关注第 48 到 52 行的循环体:

如果运行结果出错,请优先检查这几行语句的执行顺序。调试是提升编程能力的重要途径。
作者在实践中发现,M 的值在某些情况下无需参与迭代更新,仍可得到正确结果。经少量测试验证可行,现分享出来供大家分析、讨论、指正。

最小公倍数的求解
一旦获得了最大公约数,求最小公倍数就变得非常简单。
考试时作者曾忘记公式,只能盯着测试样例反复观察——“瞪眼法”最终奏效:原来最小公倍数 = (a / GCD) × b。
换句话说,两数乘积除以最大公约数,即可得最小公倍数。

可,可,可,可,可……致敬经典电影中的那一幕!
边界处理与断言机制
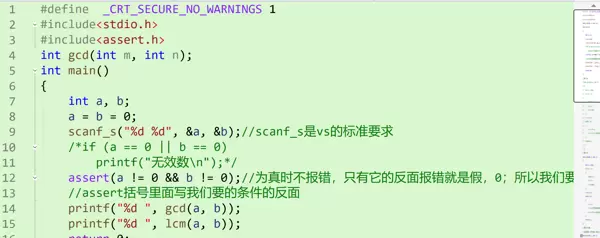
需要注意的是,输入的两个数不能为 0,否则最大公约数失去意义。
可以用 if 进行判断,但作者推荐使用 assert 断言宏,需包含头文件 <assert.h>。
也许你会问:宏是什么?断言又是什么?
简单来说,断言用于验证程序中的假设是否成立。一旦条件不满足,程序会报错并终止,帮助开发者快速定位问题。

学习是一个逐步积累的过程,一点一滴汇聚成海。保持耐心,持续进步。
拓展思考:多个数的 GCD 与 LCM
对于多个整数的最大公约数和最小公倍数,核心思想是“化繁为简,化多元为二元”。
可以先求前两个数的 GCD,再将其结果与第三个数求 GCD,依次类推。LCM 同理。
希望你在掌握基础的同时,也能发展自己的思维方式,勇于创新,乐于分享。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







