Python 可视化进阶：用 Matplotlib 绘制安德鲁斯曲线（高维世界杯数据可视化实战）

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

安德鲁斯曲线（Andrews Curves）是一种高效处理高维数据可视化的工具，能够将多维特征转化为二维空间中的连续函数曲线。通过观察这些曲线的形态、趋势以及聚类情况，可以直观地识别不同类别之间的差异性。相较于平行坐标图或散点图矩阵，该方法更擅长揭示数据整体结构，在分类分析、特征分组和异常检测中具有广泛应用。 本文以1930至2014年世界杯球队的多维度表现数据为案例，深入解析如何使用 Matplotlib 实现安德鲁斯曲线，并挖掘冠军队与非冠军队在战术与战绩特征上的潜在规律。

一、核心原理与实际应用

1. 基本思想

安德鲁斯曲线的核心基于傅里叶级数展开：将一个 n 维向量 \( (x_1, x_2, ..., x_n) \) 映射成定义在区间 \( t \in [-\pi, \pi] \) 上的连续函数： \[ f(t) = \frac{x_1}{\sqrt{2}} + x_2 \sin(t) + x_3 \cos(t) + x_4 \sin(2t) + x_5 \cos(2t) + \cdots \] 每个维度的数值作为傅里叶项的系数，最终生成一条随 t 变化的平滑曲线。 由于相同类别的样本往往具有相似的特征分布，因此它们所对应的曲线通常会形成聚集区域；而不同类别的曲线则表现出明显的形状分离，便于进行模式识别。

2. 主要应用场景

• 分类验证：判断现有标签是否合理，例如对比世界杯“冠军队”与“非冠军队”的综合能力差异；
• 特征聚类：探索未知分组结构，如按大洲划分球队时是否存在战术风格趋同现象；
• 异常检测：识别偏离主流群体的孤立曲线，可能对应冷门球队或特殊战术打法。

本文聚焦于“冠军 vs 非冠军”球队的多维特征对比，使可视化结果更具现实解释力。

二、环境配置与数据准备

1. 所需依赖库安装

实现安德鲁斯曲线需借助以下 Python 库： - Pandas：用于数据读取与预处理； - Matplotlib：绘制曲线图形； - Scipy：支持数学函数计算； - Scikit-learn：执行特征标准化，消除量纲影响。 可通过如下命令完成安装：

pip install matplotlib pandas scipy scikit-learn

2. 数据集说明

采用模拟但符合真实赛事逻辑的世界杯球队数据集，包含8支曾夺冠球队与12支未夺冠球队，共5个关键指标：

特征名称	说明	量纲
avg_goals	场均进球数	个 / 场
avg_concede	场均失球数	个 / 场
avg_yellow	场均黄牌数	张 / 场
win_rate	胜率（胜场 / 总场数）	%
half_win_rate	半场领先后获胜的比例	%

部分数据展示如下：

team               avg_goals  avg_concede  avg_yellow  win_rate  half_win_rate  is_champion
巴西（1970）         2.8        0.8          1.2         85        90             1
德国（1990）         2.0        0.7          1.5         80        88             1
日本（2002）         1.1        1.2          1.8         33        60             0
韩国（2002）         1.0        1.1          2.0         40        65             0

三、基础实现流程

1. 关键步骤

• 对原始特征进行标准化处理，防止高数值变量主导曲线形态；
• 构建 \( t \in [-\pi, \pi] \) 的等距序列；
• 依据安德鲁斯公式计算每条样本的函数输出值；
• 根据类别（是否为冠军）分别绘制曲线，统一颜色编码。

2. 基础代码示例

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler

# ---------------------- 1. 数据准备与预处理 ----------------------
# 模拟世界杯球队多维数据
data = {
    "team": ["巴西(1970)", "德国(1990)", "阿根廷(1986)", "法国(1998)", "意大利(2006)", 
             "西班牙(2010)", "乌拉圭(1930)", "英格兰(1966)", "日本(2002)", "韩国(2002)",
             "墨西哥(1986)", "比利时(2014)", "瑞士(2014)", "瑞典(2006)", "智利(2010)",
             "哥伦比亚(2014)", "尼日利亚(1994)", "喀麦隆(1990)", "美国(1994)", "澳大利亚(2006)"],
    "avg_goals": [2.8, 2.1, 2.5, 2.3, 1.9, 2.0, 2.2, 2.4, 1.0, 1.1, 1.2, 1.5, 1.3, 1.4, 1.2, 1.6, 1.0, 0.9, 1.1, 0.8],
    "avg_concede": [0.8, 0.7, 0.9, 0.8, 0.6, 0.5, 1.0, 0.8, 1.2, 1.1, 1.1, 0.9, 1.0, 1.1, 1.3, 1.0, 1.2, 1.4, 1.3, 1.5],
    "avg_yellow": [1.2, 1.5, 1.1, 1.3, 1.4, 1.2, 1.6, 1.3, 1.8, 2.0, 1.7, 1.5, 1.6, 1.7, 1.9, 1.4, 1.8, 2.1, 1.7, 1.9],
    "win_rate": [85, 80, 82, 78, 81, 83, 75, 79, 33, 40, 38, 55, 45, 42, 39, 50, 35, 28, 36, 30],
    "half_win_rate": [90, 88, 89, 85, 87, 86, 80, 84, 60, 65, 62, 70, 68, 66, 61, 69, 58, 55, 60, 56],
    "is_champion": [1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
}
df = pd.DataFrame(data)

# 提取特征列（排除非数值列）
features = ["avg_goals", "avg_concede", "avg_yellow", "win_rate", "half_win_rate"]
X = df[features].values

# 标准化（关键：消除量纲影响，比如胜率是百分比，进球数是个位数）
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
df_scaled = pd.DataFrame(X_scaled, columns=features)
df_scaled["is_champion"] = df["is_champion"]
df_scaled["team"] = df["team"]

# ---------------------- 2. 生成安德鲁斯曲线的t值与曲线值 ----------------------
# 生成t序列（范围[-π, π]，取1000个点保证曲线平滑）
t = np.linspace(-np.pi, np.pi, 1000)

# 定义安德鲁斯曲线计算函数
def andrews_curve(row, t):
    """
    计算单条安德鲁斯曲线的y值
    row: 标准化后的特征行（一维数组）
    t: t值序列
    """
    n = len(row)
    y = row[0] / np.sqrt(2)  # 第一项：x1/√2
    for i in range(1, n):
        if i % 2 == 1:  # 奇数项：sin(k*t)，k = (i+1)/2
            k = (i + 1) // 2
            y += row[i] * np.sin(k * t)
        else:  # 偶数项：cos(k*t)，k = i/2
            k = i // 2
            y += row[i] * np.cos(k * t)
    return y

# ---------------------- 3. 绘制安德鲁斯曲线 ----------------------
# 设置中文显示
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

# 创建画布
fig, ax = plt.subplots(figsize=(14, 8))

# 按类别绘制曲线：冠军队（红色）、非冠军队（蓝色）
# 冠军队曲线
champion_data = df_scaled[df_scaled["is_champion"] == 1]
for idx, row in champion_data.iterrows():
    y = andrews_curve(row[features].values, t)
    ax.plot(t, y, color="#d62728", alpha=0.7, linewidth=1.5, label="冠军队" if idx == champion_data.index[0] else "")

# 非冠军队曲线
non_champion_data = df_scaled[df_scaled["is_champion"] == 0]
for idx, row in non_champion_data.iterrows():
    y = andrews_curve(row[features].values, t)
    ax.plot(t, y, color="#1f77b4", alpha=0.5, linewidth=1, label="非冠军队" if idx == non_champion_data.index[0] else "")

# ---------------------- 4. 图表基础美化 ----------------------
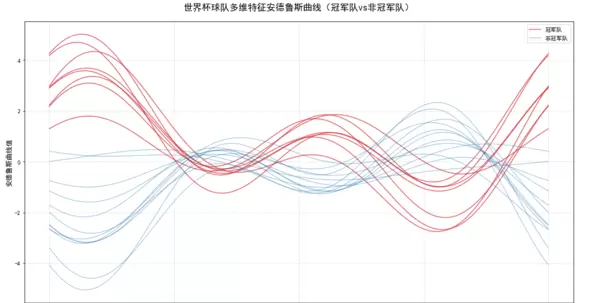
ax.set_title("世界杯球队多维特征安德鲁斯曲线（冠军队vs非冠军队）", fontsize=16, pad=20)
ax.set_xlabel("t（弧度）", fontsize=12)
ax.set_ylabel("安德鲁斯曲线值", fontsize=12)
ax.grid(True, linestyle="--", alpha=0.5)

# 添加图例（避免重复）
ax.legend(loc="upper right", fontsize=10)

# 调整x轴刻度为π的倍数，更易解读
ax.set_xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi])
ax.set_xticklabels(["-π", "-π/2", "0", "π/2", "π"], fontsize=10)

plt.tight_layout()
plt.show()

运行上述代码后得到的基础可视化图像如下：

3. 结果分析

从图表中可观察到： - 红色曲线（代表冠军队）高度集中，表明其各项指标具备较强一致性； - 蓝色曲线（非冠军队）分布广泛且波动剧烈，体现其表现多样性； - 在 \( t=0 \) 和 \( t=\pi/2 \) 等关键位置，两类曲线存在显著差距，反映出胜率、进球效率等核心特征的系统性差异。

四、进阶优化与深度解读

1. 提升可视化的清晰度与信息量

• 标注代表性球队（如巴西、德国），增强可读性；
• 添加平均曲线（粗线表示），突出组间总体趋势；
• 调整线条透明度与样式，缓解重叠干扰；
• 结合时间节点解释各段曲线对应的物理意义。

2. 进阶代码实现

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler

# ---------------------- 1. 数据预处理（同基础版） ----------------------
data = {
    "team": ["巴西(1970)", "德国(1990)", "阿根廷(1986)", "法国(1998)", "意大利(2006)", 
             "西班牙(2010)", "乌拉圭(1930)", "英格兰(1966)", "日本(2002)", "韩国(2002)",
             "墨西哥(1986)", "比利时(2014)", "瑞士(2014)", "瑞典(2006)", "智利(2010)",
             "哥伦比亚(2014)", "尼日利亚(1994)", "喀麦隆(1990)", "美国(1994)", "澳大利亚(2006)"],
    "avg_goals": [2.8, 2.1, 2.5, 2.3, 1.9, 2.0, 2.2, 2.4, 1.0, 1.1, 1.2, 1.5, 1.3, 1.4, 1.2, 1.6, 1.0, 0.9, 1.1, 0.8],
    "avg_concede": [0.8, 0.7, 0.9, 0.8, 0.6, 0.5, 1.0, 0.8, 1.2, 1.1, 1.1, 0.9, 1.0, 1.1, 1.3, 1.0, 1.2, 1.4, 1.3, 1.5],
    "avg_yellow": [1.2, 1.5, 1.1, 1.3, 1.4, 1.2, 1.6, 1.3, 1.8, 2.0, 1.7, 1.5, 1.6, 1.7, 1.9, 1.4, 1.8, 2.1, 1.7, 1.9],
    "win_rate": [85, 80, 82, 78, 81, 83, 75, 79, 33, 40, 38, 55, 45, 42, 39, 50, 35, 28, 36, 30],
    "half_win_rate": [90, 88, 89, 85, 87, 86, 80, 84, 60, 65, 62, 70, 68, 66, 61, 69, 58, 55, 60, 56],
    "is_champion": [1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
}
df = pd.DataFrame(data)
features = ["avg_goals", "avg_concede", "avg_yellow", "win_rate", "half_win_rate"]
X = df[features].values
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
df_scaled = pd.DataFrame(X_scaled, columns=features)
df_scaled["is_champion"] = df["is_champion"]
df_scaled["team"] = df["team"]

# ---------------------- 2. 安德鲁斯曲线计算 + 平均曲线 ----------------------
t = np.linspace(-np.pi, np.pi, 1000)

def andrews_curve(row, t):
    n = len(row)
    y = row[0] / np.sqrt(2)
    for i in range(1, n):
        if i % 2 == 1:
            k = (i + 1) // 2
            y += row[i] * np.sin(k * t)
        else:
            k = i // 2
            y += row[i] * np.cos(k * t)
    return y

# 计算冠军队/非冠军队的平均曲线
champion_X = df_scaled[df_scaled["is_champion"] == 1][features].values
champion_avg = np.mean(champion_X, axis=0)
champion_avg_curve = andrews_curve(champion_avg, t)

non_champion_X = df_scaled[df_scaled["is_champion"] == 0][features].values
non_champion_avg = np.mean(non_champion_X, axis=0)
non_champion_avg_curve = andrews_curve(non_champion_avg, t)

# ---------------------- 3. 精细化绘制 ----------------------
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
fig, ax = plt.subplots(figsize=(16, 9))

# 1. 绘制所有样本曲线（低透明度）
# 冠军队
champion_data = df_scaled[df_scaled["is_champion"] == 1]
for idx, row in champion_data.iterrows():
    y = andrews_curve(row[features].values, t)
    ax.plot(t, y, color="#d62728", alpha=0.4, linewidth=1)

# 非冠军队
non_champion_data = df_scaled[df_scaled["is_champion"] == 0]
for idx, row in non_champion_data.iterrows():
    y = andrews_curve(row[features].values, t)
    ax.plot(t, y, color="#1f77b4", alpha=0.3, linewidth=1)

# 2. 绘制平均曲线（加粗+醒目颜色）
ax.plot(t, champion_avg_curve, color="#e74c3c", linewidth=3, label="冠军队平均曲线")
ax.plot(t, non_champion_avg_curve, color="#3498db", linewidth=3, label="非冠军队平均曲线")

# 3. 标注经典冠军队曲线（巴西、德国）
brazil_row = df_scaled[df_scaled["team"] == "巴西(1970)"][features].values[0]
brazil_curve = andrews_curve(brazil_row, t)
ax.plot(t, brazil_curve, color="#c0392b", linewidth=2.5, linestyle="--", label="巴西(1970)")

germany_row = df_scaled[df_scaled["team"] == "德国(1990)"][features].values[0]
germany_curve = andrews_curve(germany_row, t)
ax.plot(t, germany_curve, color="#e67e22", linewidth=2.5, linestyle="--", label="德国(1990)")

# ---------------------- 4. 高级美化与解读 ----------------------
# 标题与标签
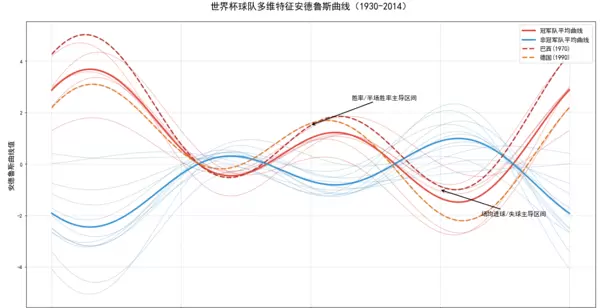
ax.set_title("世界杯球队多维特征安德鲁斯曲线（1930-2014）", fontsize=18, pad=25)
ax.set_xlabel("t（弧度）", fontsize=14)
ax.set_ylabel("安德鲁斯曲线值", fontsize=14)

# x轴刻度优化
ax.set_xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi])
ax.set_xticklabels(["-π", "-π/2", "0", "π/2", "π"], fontsize=12)

# 网格与图例
ax.grid(True, linestyle="--", alpha=0.6)
ax.legend(loc="upper right", fontsize=12, framealpha=0.9)

# 添加关键节点解读标注
ax.annotate(
    "胜率/半场胜率主导区间", 
    xy=(0, 1.5), xytext=(0.5, 2.5),
    arrowprops=dict(arrowstyle="->", color="black", lw=1.5),
    fontsize=12, fontweight="bold"
)
ax.annotate(
    "场均进球/失球主导区间", 
    xy=(np.pi/2, -1), xytext=(np.pi/2 + 0.5, -2),
    arrowprops=dict(arrowstyle="->", color="black", lw=1.5),
    fontsize=12, fontweight="bold"
)

plt.tight_layout()
# 导出高清图片（可选）
plt.savefig("worldcup_andrews_curve.png", dpi=300, bbox_inches="tight")
plt.show()

优化后的效果图如下所示：

3. 深层洞察

• 平均曲线对比：红色粗线（冠军平均）与蓝色粗线（非冠军平均）之间差距明显，直接反映两类球队的整体实力落差；
• 典型球队定位：巴西与德国的曲线紧贴冠军平均线，印证其典型的“冠军级”表现模式；
• 关键区段解析：
  • 在 \( t=0 \) 附近，函数主要受 \( win\_rate \) 与 \( half\_win\_rate \) 影响，此处冠军队值更高，说明心理优势与控场能力强；
  • 在 \( t=\pi/2 \) 区域，\( avg\_goals \) 与 \( avg\_concede \) 起主导作用，冠军队曲线更平稳，体现攻守均衡。

五、常见问题及应对策略

1. 曲线过度重叠导致难以辨识

• 方案一：降低单条曲线的透明度（alpha值），同时强化平均曲线显示效果；

  alpha=0.3-0.5

• 方案二：先对特征进行降维（如 PCA），再绘制低维映射后的安德鲁斯曲线，减少复杂度；
• 方案三：按子群拆分绘图，例如按年代或地理区域分别绘制。

2. 量纲不一致引发偏差

若不对数据进行归一化或标准化处理，某些量级较大的特征（如胜率以百分比计）会严重扭曲曲线形态。 解决办法：必须在绘图前对所有特征执行标准化（StandardScaler）或归一化（MinMaxScaler）处理。

StandardScaler

MinMaxScaler

3. 更进一步的优化方向

• 引入交互功能：利用特定可视化库实现鼠标悬停显示具体球队名称；

  mpl_interactions

• 动态控制维度输入：加入滑动条控件，允许用户选择参与计算的特征组合，实时查看曲线变化。

六、总结与拓展

安德鲁斯曲线作为 Matplotlib 可视化体系中的重要组成部分，是进行高维数据探索的有效手段。本文以世界杯球队的多维数据为案例，系统展示了从基础绘图到细节优化的完整实现流程，深入剖析了该方法在实际场景中的应用价值。

多子图对比分析：将年代划分为两个阶段（1930–1970 年和 1971–2014 年），分别绘制子图，通过观察曲线形态的演变趋势，揭示不同历史时期的数据特征变化规律。

拓展应用场景：

• 赛事分析：对世界杯历届比赛的关键指标（如场均进球数、红黄牌数量、现场观众规模等）进行年代间对比，识别赛事风格的长期变迁；
• 财务分析：用于跨行业企业财务状况的多维度比较，涵盖营收水平、盈利能力和负债比例等核心指标；
• 用户分析：在电商领域中，依据用户的多维行为数据（包括页面浏览、商品加购、订单提交等）实现用户群体的有效划分与画像构建。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：Matplotlib matplot python 数据可视化 plot

相关内容：Python数据可视化实战 Python数据可视化可视化 Python可视化实战