我见过的最好的各统计分布之间关系的整理

相似文件 换一批

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

论坛好像没有这篇文章。虽然是转发过来的，但超链接等经过了我精心的编辑。求评分！加精就更好了。英语阅读稍有困难的，推荐“灵格斯”划词翻译。

---

Diagram of distribution relationships

Probability distributions have a surprising number inter-connections. A dashed line in the chart below indicates an approximate (limit) relationship between two distribution families. A solid line indicates an exact relationship: special case, sum, or transformation.

Click on a distribution for the parameterization of that distribution. Click on an arrow for details on the relationship represented by the arrow. Other diagrams on this site:

The chart above is adapted from the chart originally published by Lawrence Leemis in 1986 (Relationships Among Common Univariate Distributions, American Statistician 40:143-146.) Leemis published a larger chart in 2008 which is available online.

Parameterizations

The precise relationships between distributions depend on parameterization. The relationships detailed below depend on the following parameterizations for the PDFs.

Let C(n, k) denote the binomial coefficient(n, k) and B(a, b) = Γ(a) Γ(b) / Γ(a + b).

Geometric: f(x) = p (1-p)x for non-negative integers x.

Discrete uniform: f(x) = 1/n for x = 1, 2, ..., n.

Negative binomial: f(x) = C(r + x - 1, x) pr(1-p)x for non-negative integers x. See notes on the negative binomial distribution.

Beta binomial: f(x) = C(n, x) B(α + x, n + β - x) / B(α, β) for x = 0, 1, ..., n.

Hypergeometric: f(x) = C(M, x) C(N-M, K - x) / C(N, K) for x = 0, 1, ..., N.

Poisson: f(x) = exp(-λ) λx/ x! for non-negative integers x. The parameter λ is both the mean and the variance.

Binomial: f(x) = C(n, x) px(1 - p)n-x for x = 0, 1, ..., n.

Bernoulli: f(x) = px(1 - p)1-x where x = 0 or 1.

Lognormal: f(x) = (2πσ2)-1/2 exp( -(log(x) - μ)2/ 2σ2) / x for positive x. Note that μ and σ2are not the mean and variance of the distribution.

Normal : f(x) = (2π σ2)-1/2 exp( - ½((x - μ)/σ)2 ) for all x.

Beta: f(x) = Γ(α + β) xα-1(1 - x)β-1 / (Γ(α) Γ(β)) for 0 ≤ x ≤ 1.

Standard normal: f(x) = (2π)-1/2 exp( -x2/2) for all x.

Chi-squared: f(x) = x-ν/2-1 exp(-x/2) / Γ(ν/2) 2ν/2 for positive x. The parameter ν is called the degrees of freedom.

Gamma: f(x) = β-α xα-1 exp(-x/β) / Γ(α) for positive x. The parameter α is called the shape and β is the scale.

Uniform: f(x) = 1 for 0 ≤ x ≤ 1.

Cauchy: f(x) = σ/(π( (x - μ)2 + σ2) ) for all x. Note that μ and σ are location and scale parameters. The Cauchy distribution has no mean or variance.

Snedecor F: f(x) is proportional to x(ν1 - 2)/2 / (1 + (ν1/ν2) x)(ν1 + ν2)/2 for positive x.

Exponential: f(x) = exp(-x/μ)/μ for positive x. The parameter μ is the mean.

Student t: f(x) is proportional to (1 + (x2/ν))-(ν + 1)/2 for positive x. The parameter ν is called the degrees of freedom.

Weibull: f(x) = (γ/β) xγ-1 exp(- xγ/β) for positive x. The parameter γ is the shape and β is the scale.

Double exponential : f(x) = exp(-|x-μ|/σ) / 2σ for all x. The parameter μ is the location and mean; σ is the scale.

For comparison, see distribution parameterizations in R/S-PLUS and Mathematica.

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享3 收藏203 回帖

关键词：统计分布 最好的 distribution relationship proportional 统计分布 关系 泊松 计量 统计

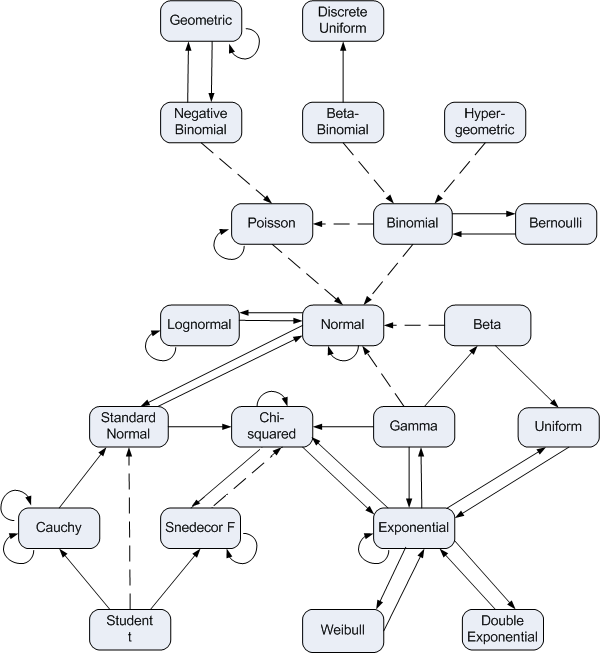
Relationships
In all statements about two random variables, the random variables are implicitly independent.

Geometric / negative binomial: If each Xi is geometric random variable with probability of success p then the sum of n Xi's is a negative binomial random variable with parameters n and p.

Negative binomial / geometric: A negative binomial distribution with r = 1 is a geometric distribution.

Negative binomial / Poisson: If X has a negative binomial random variable with r large, p near 1, and r(1-p) = λ, then FX ≈ FY where Y is a Poisson random variable with mean λ.

Beta-binomial / discrete uniform: A beta-binomial (n, 1, 1) random variable is a discrete uniform random variable over the values 0 ... n.

Beta-binomial / binomial: Let X be a beta-binomial random variable with parameters (n, α, β). Let p = α/(α + β) and suppose α + β is large. If Y is a binomial(n, p) random variable then FX ≈ FY.

Hypergeometric / binomial: The difference between a hypergeometric distribution and a binomial distribution is the difference between sampling without replacement and sampling with replacement. As the population size increases relative to the sample size, the difference becomes negligible.

Geometric / geometric: If X1 and X2 are geometric random variables with probability of success p1 and p2 respectively, then min(X1, X2) is a geometric random variable with probability of success p = p1 + p2 - p1 p2. The relationship is simpler in terms of failure probabilities: q = q1 q2.

Poisson / Poisson: If X1 and X2 are Poisson random variables with means μ1 and μ2respectively, then X1 + X2 is a Poisson random variable with mean μ1 + μ2.

Binomial / Poisson: If X is a binomial(n, p) random variable and Y is a Poisson(np) distribution then P(X = n) ≈ P(Y = n) if n is large and np is small. For more information, seePoisson approximation to binomial.

Binomial / Bernoulli: If X is a binomial(n, p) random variable with n = 1, X is a Bernoulli(p) random variable.

Bernoulli / Binomial: The sum of n Bernoulli(p) random variables is a binomial(n, p) random variable.

Poisson / normal: If X is a Poisson random variable with large mean and Y is a normal distribution with the same mean and variance as X, then for integers j and k, P(j ≤ X ≤ k) ≈ P(j - 1/2 ≤ Y ≤ k + 1/2). For more information, see normal approximation to Poisson.

Binomial / normal: If X is a binomial(n, p) random variable and Y is a normal random variable with the same mean and variance as X, i.e. np and np(1-p), then for integers j and k, P(j ≤ X ≤ k) ≈ P(j - 1/2 ≤ Y ≤ k + 1/2). The approximation is better when p ≈ 0.5 and when n is large. For more information, see normal approximation to binomial.

Lognormal / lognormal: If X1 and X2 are lognormal random variables with parameters (μ1, σ12) and (μ2, σ22) respectively, then X1 X2 is a lognormal random variable with parameters (μ1 + μ2, σ12 + σ22).

Normal / lognormal: If X is a normal (μ, σ2) random variable then eX is a lognormal (μ, σ2) random variable. Conversely, if X is a lognormal (μ, σ2) random variable then log X is a normal (μ, σ2) random variable.

Beta / normal: If X is a beta random variable with parameters α and β equal and large, FX ≈ FY where Y is a normal random variable with the same mean and variance as X, i.e. mean α/(α + β) and variance αβ/((α+β)2(α + β + 1)). For more information, see normal approximation to beta.

Normal / standard normal: If X is a normal(μ, σ2) random variable then (X - μ)/σ is a standard normal random variable. Conversely, If X is a normal(0,1) random variable then σ X + μ is a normal (μ, σ2) random variable.

Normal / normal: If X1 is a normal (μ1, σ12) random variable and X2 is a normal (μ2, σ22) random variable, then X1 + X2 is a normal (μ1 + μ2, σ12 + σ22) random variable.

Gamma / normal: If X is a gamma(α, β) random variable and Y is a normal random variable with the same mean and variance as X, then FX ≈ FY if the shape parameter α is large relative to the scale parameter β. For more information, see normal approximation to gamma.

Gamma / beta: If X1 is gamma(α1, 1) random variable and X2 is a gamma (α2, 1) random variable then X1/(X1 + X2) is a beta(α1, α2) random variable. More generally, if X1 is gamma(α1, β1) random variable and X2 is gamma(α2, β2) random variable then β2 X1/(β2 X1 + β1 X2) is a beta(α1, α2) random variable.

Beta / uniform: A beta random variable with parameters α = β = 1 is a uniform random variable.

Chi-squared / chi-squared: If X1 and X2 are chi-squared random variables with ν1 and ν2 degrees of freedom respectively, then X1 + X2 is a chi-squared random variable with ν1 + ν2 degrees of freedom.

Standard normal / chi-squared: The square of a standard normal random variable has a chi-squared distribution with one degree of freedom. The sum of the squares of n standard normal random variables is has a chi-squared distribution with n degrees of freedom.

Gamma / chi-squared: If X is a gamma (α, β) random variable with α = ν/2 and β = 2, then X is a chi-squared random variable with ν degrees of freedom.

Cauchy / standard normal: If X and Y are standard normal random variables, X/Y is a Cauchy(0,1) random variable.

Student t / standard normal: If X is a t random variable with a large number of degrees of freedom ν then FX ≈ FY where Y is a standard normal random variable. For more information, see normal approximation to t.

Snedecor F / chi-squared: If X is an F(ν, ω) random variable with ω large, then ν X is approximately distributed as a chi-squared random variable with ν degrees of freedom.

Chi-squared / Snedecor F: If X1 and X2 are chi-squared random variables with ν1 and ν2 degrees of freedom respectively, then (X1/ν1)/(X2/ν2) is an F(ν1, ν2) random variable.

Chi-squared / exponential: A chi-squared distribution with 2 degrees of freedom is an exponential distribution with mean 2.

Exponential / chi-squared: An exponential random variable with mean 2 is a chi-squared random variable with two degrees of freedom.

Gamma / exponential: The sum of n exponential(β) random variables is a gamma(n, β) random variable.

Exponential / gamma: A gamma distribution with shape parameter α = 1 and scale parameter β is an exponential(β) distribution.

Exponential / uniform: If X is an exponential random variable with mean λ, then exp(-X/λ) is a uniform random variable. More generally, sticking any random variable into its CDF yields a uniform random variable.

Uniform / exponential: If X is a uniform random variable, -λ log X is an exponential random variable with mean λ. More generally, applying the inverse CDF of any random variable X to a uniform random variable creates a variable with the same distribution as X.

Cauchy reciprocal: If X is a Cauchy (μ, σ) random variable, then 1/X is a Cauchy (μ/c, σ/c) random variable where c = μ2 + σ2.

Cauchy sum: If X1 is a Cauchy (μ1, σ1) random variable and X2 is a Cauchy (μ2, σ2), then X1 + X2 is a Cauchy (μ1 + μ2, σ1 + σ2) random variable.

Student t / Cauchy: A random variable with a t distribution with one degree of freedom is a Cauchy(0,1) random variable.

Student t / Snedecor F: If X is a t random variable with ν degree of freedom, then X2 is an F(1,ν) random variable.

Snedecor F / Snedecor F: If X is an F(ν1, ν2) random variable then 1/X is an F(ν2, ν1) random variable.

Exponential / Exponential: If X1 and X2 are exponential random variables with mean μ1 and μ2 respectively, then min(X1, X2) is an exponential random variable with mean μ1 μ2/(μ1 + μ2).

Exponential / Weibull: If X is an exponential random variable with mean β, then X1/γis a Weibull(γ, β) random variable.

Weibull / Exponential: If X is a Weibull(1, β) random variable, X is an exponential random variable with mean β.

Exponential / Double exponential: If X and Y are exponential random variables with mean μ, then X-Y is a double exponential random variable with mean 0 and scale μ

Double exponential / exponential: If X is a double exponential random variable with mean 0 and scale λ, then |X| is an exponential random variable with mean λ.

这么专业的东西，我只能说：不明觉厉啊！

必须赞一下，回来一定好好研究

这是一篇文章的，一个是1986年的，另一个是2008年更新的
Univariate Distribution Relationships
http://www.math.wm.edu/~leemis/2008amstat.pdf

蓝色 发表于 2014-3-10 14:00
这是一篇文章的
Univariate Distribution Relationships
http://www.math.wm.edu/~leemis/2008amstat.pdf ...

蓝版主果然厉害。pdf里的那个图更震撼……

蓝色 发表于 2014-3-10 14:00
这是一篇文章的
Univariate Distribution Relationships
http://www.math.wm.edu/~leemis/2008amstat.pdf ...

是的，蓝色版主，在图下第一段已说明。我觉得这样帖子的形式，在文中加入超链接，学习起来感觉更方便，就分享给大家了。版主厉害。

这个整理不错！我记得以前看到有本书专门介绍各种分布的，像概率分布百科全书一样。

还看到过有本书专门讲统计检验的，各种各样的检验都有，像统计检验百科全书一样。

Crsky7 发表于 2014-3-10 14:18
还看到过有本书专门讲统计检验的，各种各样的检验都有，像统计检验百科全书一样。

Crsky7版主，你可以回忆一下是哪本书，给大家分享一下呀。