发帖
雷达卡
什么是辛普森悖论？
我们先用一个例子来说明到底什么是辛普森悖论。
假设上表是北京大学和清华大学的男女学生比例，可以发现：北大男生有95人，女生有209人，男女学生比例为0.45:1；清华男生有110人，女生有143人，男女学生比例为0.77:1。根据上面这一数据，我们基本可以得到如下结论：尽管北大和清华都是阴盛阳衰，但明显北大更严重啊！
那事实果真如是吗？
考虑到北大更偏重文科专业，而清华更偏重理工科专业。我们把样本按理工科和文科进一步进行分类，得到下面这张表：
可以看出：北大的理工科男女比例是5.6:1，文科的男女比例是0.25:1；清华的理工科男女比例是2.0:1，文科的男女比例是0.10:1。发现问题了吗？跟清华相比，北大的理工科和文科的都是男生人数要多啊？？？
这是怎么回事？
这就是辛普森悖论！
为什么会出现辛普森悖论？
用文绉绉的话说，这是由于混合样本中可能包含着类型完全不同的个体，因此，全样本的分析并不能代表其中每类个体的特征，特别是当个体间在被解释变量上存在巨大差异以及不同个体的样本总数存在巨大差异的时候，辛普森悖论就更会产生。
以上面的数据为例，理工科、文科的男女性别比例本身就有很大差异，读理工科的男生多，读文科的女生多，这在北大和清华都是如此；同时，由于北大作为文科为主的学校，所以招收了更多的女生，清华作为理工科为主的学校，招收了更多的男生。那么，当北大样本中包含更多女生，清华样本中包含更多男生时，我们就会看到一开始的那种表：北大阴盛阳衰啊！
辛普森悖论告诉我们什么道理？
对关键变量，特别是直接影响被解释变量的变量，一定要对其进行细分，然后才能得到正确的结论！否则结论往往可能是错的！
知道辛普森悖论后，我们就应该做出更正确的决策！
我们再来看一个例子。
这是一个移动应用程序的所有用户数据，其中1万人使用Android设备，5千人使用iOS设备。用户中iOS设备的转化率是4%，Android设备的转化率是5.5%。据此，我们会做出如下决策：优先开发Android设备。
莫急！
知道了辛普森悖论以后，我们就应该考虑的更细致，因为平板设备和手机设备的转化率完全不同，而且使用平板设备和使用手机设备的人数也完全不同，所以我们一定要按设备类型对样本进行细分。
再看如下数据：
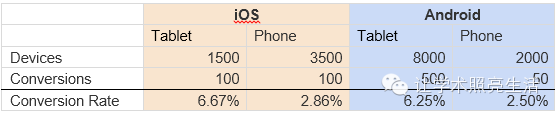
可以发现：iOS平板的转换率比Android平板高一点，iOS手机的转换率同样比Android手机高。
这样子产品经理的决策可能就会不同了。
为什么辛普森悖论会让许多学术研究的结论变得不可靠？
终于回到了一开始我们提出的问题，为什么辛普森悖论会让许多学术研究的结论变得不可靠？核心原因就是遗漏变量问题。
因为存在遗漏变量，因为对遗漏变量没有细分，我们就可能得到一些总样本上看似合理，但细分样本后却完全错误的结论。
京公网安备 11010802022788号
