发帖
雷达卡
Ho-Lee模型是指什么_Ho-Lee模型的基本假设_Ho-Lee模型的主要内容
Ho-Lee模型是指什么
1986年托马斯·侯（Thomas.Y.Ho）和李尚宾（Sang-bing.Lee）二人在美国《金融杂志》12月号上发表了论文《期限结构运动与利率有条件要求权定价》，文章中提出了一个基于无套利机会假设的利率期限结构变动模型，人们称之为Ho-Lee模型。
Ho-Lee模型认为现在的利率期限结构包含有现时人们对利率预测的足够信息，因此在没有套利机会的假设下，利率期限结构的变动只能反映出这些信息，因而其变化情况是可测的。Ho-Lee模型分成两个部分，一是利率期限结构变动的模型，另一部分是该模型在利率期权定价中的应用。
[编辑]
二元格点结构
Ho-Lee模型考察贴现函数的变动，其最重要的部分是贴现函数的二元格点结构。对于贴现函数Ds,t( * )，在初始时刻为零状态，记为D( * ) = D0.0( * )，经过一时刻后，在时刻1，贴现函数可能出现两种状态：上升状态和下降状态，贴现函数分别为D1.1( * )和D0.1( * )，以后每经历一个上升状态，状态下标s增加1，否则不增加；时间下标t在每一时刻后增加1。这样，在时刻2有贴现函数D2.2( * )，D1,2( * )和D0,2( * )。显然，这里出现一种路径无关现象，即贴现函数经历一次上升后下降D0,0( * ) − − D1,1( * ) − − D1,2( * )和经历一次下降后上升D0,0( * ) − − D0,1( * ) − − D1,2( * )完全相同，Ds,t(T)只与经历的上升次数和下降次数有关而与时间路径无关。Ho-Lee模型将这种现象称为贴现函数与路径无关。
通常我们用收益率曲线而不用贴现函数来表示利率期限结构，因此须将贴现函数转为收益率曲线形式，收益率曲线为：
R（T）= - LnD（T）/T （3）
其中R（T）是到期期限为T的贴现债券的连续复利收益率。
Ho-Lee模型的基本假设
Ho-Lee模型的基本假设有以下几点：
1、市场是无摩擦的，既无税收费用，也不考虑交易费用，所有证券皆可分割。
2、市场并非连续出清，而是在有规则间隔的时点上出清。模型中以一段时隔为时间单位，定义期限为T的贴现债券为到第T期末偿付1美元的债券。
3、市场是完全的。对每一期限n，均有相对应的贴现债券存在。（n=0,1,2,3……）
4、在每一时刻n，仅存在有限种状态。定义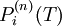
为在时刻n、状态i下期限为T的债券价格。这里，
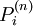是一以期限为变量的贴现债券价格函数，称为贴现函数。贴现函数必须满足下列条件：它们必须是正数，此外要求：
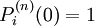(1)
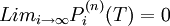(2)(1)式表明，贴现债券到期值为1美元。(2)表明期限极长的贴现债券之现值可忽略不计。
Ho-Lee模型的主要内容
Ho-Lee模型是建立在无套利假设基础上的，它现在已经成为分离时间框架基础上利率期限结构模型的一般原则。Ho-Lee模型的主要内容有：
1、初始利率期限结构的估计。首先必须确定一个期限结构或相应贴现函数的初始状态，一般来说要求所选择的债券能覆盖市场上大部分可得债券，并必须运用特定的函数形式，如指数形式。
2、利率变动的套利约束。利率期限结构被假设按满足某种自然约束的方式进行变化，Ho-Lee模型假定贴现函数依据下列原则随时间进行变化：
对所有（s,t）和T= 1,2,…,n,
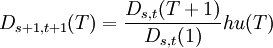(4)
和
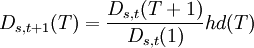(5)
其中hu(T)和hd(T)被称为扰动函数(Perturbation function )。注意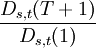
是在结点（s,t）处隐含的T期远期利率。扰动函数hu(T)和hd(T)分别衡量了期限结构中上升状态和下降状态下利率同隐含远期利率的差额，因此期限结构的波动性就隐含在扰动函数中。在Ho-Lee模型中hu(T)和hd(T)被简化为与（s,t）无关而只与T有关。依据无套利假设，有Ds,t(0) = 1 ，且Ds,t(T + 1) > Ds,t(T)，对所有（s,t）和T= 1,2,…,n；由于无套利机会，因此在点（s,t）处存在参数π，是一个不随（s,t）变化的常数，使得T期贴现函数在（s,t）的价格等于一时刻后债券价格的π权重线性组合的价值的现值，即:
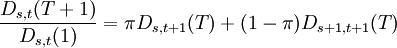，T= 1,2,…,n （6）
代入（4）、（5）式变化后，有：
πhd(T) + （1 - π）hu(T) = 1 （7）
对于某一常数π和初始贴现函数D0,0(T)，使得（7）式成立。
经过一番复杂的推导可以得到扰动函数hu(T)的唯一解为：
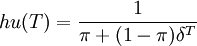（8）
将（8）代入（7）式，得：
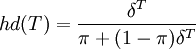（9）
这样，我们得到了扰动函数的一般表达式，只要给定参数π、δ，就可以由公式（8）、（9）得到Ho-Lee模型的一般表达式，即可由初始的贴现函数D0,0（T）和参数π、δ来完全确定利率期限结构的变化。特别地，在更复杂的Ho-Lee模型的推广模型中，参数π、δ被看作是随状态s和时间t而变化。
Ho-Lee模型中的参数π被看作是一种风险中性概率，即恰好使得本时刻的T期限债券的价格等于本时刻后预期价格现值的概率，这一点反映在（6）中，因此π=（r-d）/（u-d），这里r是无风险收益，u和d分别是上升状态和下降状态的无风险收益。参数δ的解释稍稍复杂一些，正如Ho-Lee所指出的，δ决定了两个扰动函数hu(T)和hd(T)间的差额，差额越大，则期限结构的可变性越大，因此参数δ同期限结构的可变性直接相关，而且呈负相关关系，即δ越大，波动性越小。这一点可以由（12）式可以看出:
δ= 1 /[（1 -π）hu(1)] -π/（1 -π） （10）
因此δ越大，hu(1)越小，即波动性越小。
Ho-Lee模型指出，参数π、δ的估计，必须使用非线性估计方法来决定，使得某些或有要求权的理论价格能最好地符合观察到的价格。具体来说，是通过一个反复试错的过程来估计π、δ的值。首先观察一组不同期限的或有要求权的价格，以此来计算初始的π、δ，随后用它们来估计理论价格，再依据理论价格和观察到价格之间的差价来调整π、δ，使得理论价格尽可能符合观察到的价格。这一过程一直重复下去，直到最后理论价格充分接近市场价格。
提升卡
置顶卡
沉默卡
变色卡
抢沙发
千斤顶
显身卡
京公网安备 11010802022788号
