请教关于三个相关系数的问题

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

<P>请问：Ｐearson相关系数、Ｋendall偏秩相关系数和Spearman秩相关系数的区别是什么？检验两列时间序列数据之间的相关性是不是检验Spearman秩相关系数啊？急！急！！急！！！</P>

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏1 回帖

关键词：相关系数 spearman pearman 时间序列数据 ARMA 相关性 皮尔逊相关系数 偏相关系数 pearson相关系数 相关系数检验 spearman相关系数 复相关系数 相关系数矩阵

The Kendall tau rank correlation coefficient (or simply the Kendall tau coefficient, Kendall's τ or Tau test(s)) is used to measure the degree of correspondence between two rankings and assessing the significance of this correspondence. In other words, it measures the strength of association of the cross tabulations.

The Kendall tau coefficient (τ) has the following properties:

• If the agreement between the two rankings is perfect (i.e., the two rankings are the same) the coefficient has value 1.
• If the disagreement between the two rankings is perfect (i.e., one ranking is the reverse of the other) the coefficient has value -1.
• For all other arrangements the value lies between -1 and 1, and increasing values imply increasing agreement between the rankings. If the rankings are completely independent, the coefficient has value 0.

Kendall tau coefficient is defined

where n is the number of items, and P is the sum, over all the items, of items ranked after the given item by both rankings.

P can also be interpreted as the number of concordant pairs . The denominator in the definition of τ can be interpreted as the total number of pairs of items. So, a high value of P means that most pairs are concordant, indicating that the two rankings are consistent. Note that a tied pair is not regarded as concordant or discordant. If there is a large number of ties, the total number of pairs (in the denominator of the expression of τ) should be adjusted accordingly.

Tau a - This tests the strength of association of the cross tabulations when both variables are measured at the ordinal level but makes no adjustment for ties.

Tau b - This tests the strength of association of the cross tabulations when both variables are measured at the ordinal level. It makes adjustments for ties and is most suitable for square tables. Values range from -1 (100% negative association, or perfect inversion) to +1 (100% positive association, or perfect agreement). A value of zero indicates the absence of association.

Tau c - This tests the strength of association of the cross tabulations when both variables are measured at the ordinal level. It makes adjustments for ties and is most suitable for rectangular tables. Values range from -1 (100% negative association, or perfect inversion) to +1 (100% positive association, or perfect agreement). A value of zero indicates the absence of association.

----------------------------------------------------------------------------------------------

The Pearson product-moment correlation coefficient (sometimes known as the PMCC) (r) is a measure of the correlation of two variables X and Y measured on the same object or organism, that is, a measure of the tendency of the variables to increase or decrease together. It is defined as the sum of the products of the standard scores of the two measures divided by the degrees of freedom:

Note that this formula assumes that the standard deviations on which the Z scores are based are calculated using n − 1 in the denominator.

The result obtained is equivalent to dividing the covariance between the two variables by the product of their standard deviations. In general the correlation coefficient is one of the two square roots (either positive or negative) of the coefficient of determination (r²), which is the ratio of explained variation to total variation:

where:

Y = a score on a random variable Y

Y' = corresponding predicted value of Y, given the correlation of X and Y and the value of X

= sample mean of Y (i.e., the mean of a finite number of independent observed realizations of Y, not to be confused with the expected value of Y)

The correlation coefficient adds a sign to show the direction of the relationship. The formula for the Pearson coefficient conforms to this definition, and applies when the relationship is linear.

The coefficient ranges from −1 to 1. A value of 1 shows that a linear equation describes the relationship perfectly and positively, with all data points lying on the same line and with Y increasing with X. A score of −1 shows that all data points lie on a single line but that Y increases as X decreases. A value of 0 shows that a linear model is inappropriate – that there is no linear relationship between the variables.

The Pearson coefficient is a statistic which estimates the correlation of the two given random variables.

The linear equation that best describes the relationship between X and Y can be found by linear regression. This equation can be used to "predict" the value of one measurement from knowledge of the other. That is, for each value of X the equation calculates a value which is the best estimate of the values of Y corresponding the specific value of X. We denote this predicted variable by Y.

Any value of Y can therefore be defined as the sum of Y′ and the difference between Y and Y′:

The variance of Y is equal to the sum of the variance of the two components of Y:

Since the coefficient of determination implies that s_y.x² = s_y²(1 − r²) we can derive the identity

The square of r is conventionally used as a measure of the association between X and Y. For example, if the coefficient is 0.90, then 81% of the variance of Y can be "accounted for" by changes in X and the linear relationship between X and Y.

----------------------------------------------------------------------------------------------

Spearman's rank correlation coefficient, named after Charles Spearman and often denoted by the Greek letter ρ (rho), is a non-parametric measure of correlation – that is, it assesses how well an arbitrary monotonic function could describe the relationship between two variables, without making any assumptions about the frequency distribution of the variables. Unlike the Pearson product-moment correlation coefficient, it does not require the assumption that the relationship between the variables is linear, nor does it require the variables to be measured on interval scales; it can be used for variables measured at the ordinal level.

In principle, ρ is simply a special case of the Pearson product-moment coefficient in which the data are converted to rankings before calculating the coefficient. In practice, however, a simpler procedure is normally used to calculate ρ. The raw scores are converted to ranks, and the differences d between the ranks of each observation on the two variables are calculated. ρ is then given by:

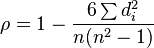
where:

d_i = the difference between each rank of corresponding values of x and y, and

n = the number of pairs of values.

Spearman's rank correlation coefficient is equivalent to Pearson correlation on ranks. The formula above is a short-cut to its product-moment form, assuming no tie. The product-moment form can be used in both tied and untied cases.

收藏了，谢谢谢谢！

学习下  偏秩相关系数

收藏，学习！

请问能有关于中文的解释吗？