R语言之高级数据分析「聚类分析」

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

聚类分析仅根据在数据中发现的描述对象及其关系的信息，将数据对象分组。其目标是，组内的对象相互之间是相似的（相关的），而不同组中的对象是不同的（不相关的）。组内相似性（同质）越大，组间差别越大，说明聚类就越好。

这一解释来自于《数据挖掘导论》，已经是大白话，很好理解了。

举个栗子：把生物按照界（Kingdom）、门（Phylum）、纲（Class）、目（Order）、科（Family）、属（Genus）、种（Species）分类。

0. 聚类分析的一般步骤

0.1. 步骤

• 选择适合的变量，选择可能对识别和理解数据中不同观测值分组有重要影响的变量。（这一步很重要，高级的聚类方法也不能弥补聚类变量选不好的问题）

• 缩放数据，一般将数据标准化处理即可，用于避免各种数据由于量纲大小不同所带来的不同

• 寻找异常点，异常点对聚类分析的结果影响很大，因此要筛选并删除

• 计算距离，后面再细讲，这个距离用于判别相关关系的大小，进而影响聚类分析的结果

• 选择聚类算法，层次聚类更适用于小样本，划分聚类更适用于较大数据量。还有许多其他的优秀算法，根据实际选择合适的。

• 得到结果，一是获得一种或多种聚类方法的结果，二是确定最终需要的类数，三是提出子群，得到最终的聚类方案

• 可视化和解读，用于展示方案的意义

• 验证结果

  
  

0.2. 计算距离

计算距离，是指运用一种合适的距离计算方式，来计算出不同观测之间的距离，这个距离用于度量观测之间的相似性或相异性。

可选的方式有欧几里得距离、曼哈顿距离、兰氏距离、非对称二元距离、最大距离和闵可夫斯基距离。

最常用的为欧几里得距离。它计算的是两个观测之间所有变量之差的平方和的开方：

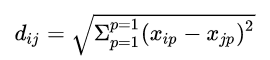
通常用于连续型数据的距离度量。

1. 划分聚类分析

将观测值分为 Ｋ 组，并根据给定的规则改组成最优粘性的类，即为划分方法。

通常有两种：K 均值和 K 中心点

1.1. K 均值聚类

K 均值聚类分析是最常见的划分方法，它使用质心来表示一个类。使用欧几里得凝聚距离，容易被异常值影响。

1.1.1 算法

1. 选择 K 个初始质心，初始质心随机选择即可，每一个质心为一个类
2. 把每个观测指派到离它最近的质心，与质心形成新的类
3. 重新计算每个类的质心，所谓质心就是一个类中的所有观测的平均向量（这里称为向量，是因为每一个观测都包含很多变量，所以我们把一个观测视为一个多维向量，维数由变量数决定）。
4. 重复2. 和 3.
5. 直到质心不在发生变化时或者到达最大迭代次数时

1.1.2. R 语言实现

• 1. 标准化数据

  
  

df <- scale(data[-1])

• 2. 决定聚类的个数

  
  

# 自编函数画碎石图，根据线性斜率变化的快慢判断聚类个数

wssplot(df)

# 用 NbClust 包中的 24 中指标来判断聚类个数

librar(NbClust)

set.seed(1234)

devAskNewPage(ask= TRUE)

nc <- NbClust(df,method= "kmeans")

table(nc$Best.n[1,])

barplot(table(nc$Best.n[1,]))# 将指标分配画可视化为条形图

• 3. 进行 K 均值聚类分析

  
  

# 3 均值聚类分析，并尝试 25 个初始中心值的配置，择其优

set.seed(1234)

fit.km <- kmeans(df, 3, nstart=25)

# 查看各聚类中的观测数量

fit$km$size

# 查看三个聚类的质心

• 4. 与原类别型变量比较

  
  

# 使用 flexclust 包中的 randIndex 函数

library(flexclust)

randIndex(fit.km)

• 如有聚类分析的数据是剔除某一类别型变量之后进行的，则要经过这一步，进行良好总分区之间的协定。兰德指数的变化范围从 -1（不同意）到 1（完全同意）。

  
  

1.2. K 中心点聚类

与 K 均值聚类不同，不用质心，而使用最具代表性的一个观测值来表示一个类，这个观测值被称为中心点。

1.2.1. 算法

1. 选择 K 个中心点，随机选择即可
2. 计算观测到各个中心点的距离或相异性
3. 把每个观测分配到最近的中心点
4. 计算每个中心点到每个观测值的距离的总和（总成本）
5. 选择一个该类中不是中心点的点，与中心点互换（它成为中心点，中心点成为普通观测）
6. 重新把每个观测分配到距它最近的中心点，组合为一个类
7. 再次计算总成本
8. 如果总成本比步骤 4. 计算的总成本少，则把新的点作为中心点
9. 重复 5. 到 8. 直到中心点不再改变

1.2.2. R 语言实现

# 使用 cluster 包中的 pam() 函数

pam(x, k, metric="euclidean", stand=FALSE)

# x为数据矩阵或者数据框，k 表示聚类的个数，metric 表示使用的相似性/相异性度量方式，stand 是否有变量在该指标之前被标准化

2. 层次聚类分析

层次聚类分析分为凝聚层次聚类分析和分裂层次聚类分析，两者是正好相反的过程，最常用到的是凝聚层次聚类分析，这篇总结只关注这一类。

其思想就是，把每一个单个的观测都视为一个类，而后计算各类之间的距离（用到 0.2. 中的方法），选取最相近的两个类，把他们合并为一个类。新的这些类再继续计算距离，合并最近的两个类。如此往复，直到只剩下一个类。将这个过程中的每一次合并都用树状图记录下来，这个树状图便包含了我们所需要的信息。

步骤可抽象为：

1. 计算类与类之间的距离，用邻近度矩阵记录
2. 将最近的两个类合并为一个新的类
3. 根据新的类，更新邻近度矩阵
4. 重复2. 3.
5. 到只只剩下一个类的时候，停止

2.1. 定义类之间的距离

观测与观测之间的距离在 0.2. 中已经说明了，有多种方式可以选择，其中最常用的就是欧几里得距离。

而类与类之间的距离，在初始的时候考虑观测之间距离是如何定义即可，因为这个时候所有类都只有一个观测。但当经过第一次合并之后，有的类就有多个观测了，这个时候类与类之间的距离应该如何定义呢？

一般有五种（下面把每个类中的观测抽象为一个点）：

1. MIN（单联动）：一个类中的所有点与另一个类中的所有点计算距离，将距离最近的两个点之间的距离视为两个类之间的距离
2. MAX（全联动）：一个类中的所有点与另一个类中的所有点计算距离，将距离最远的两个点之间的距离视为两个类之间的距离
3. 组平均（平均联动）：一个类中的所有点与另一个类中的所有点计算距离，将计算得到的所有距离相加再除以组合数所得到的平均距离视为两个类之间的距离
4. 质心：将两个类的质心之间的距离，视为两个类的距离。所谓质心就是一个类中的所有观测的平均向量（这里称为向量，是因为每一个观测都包含很多变量，所以我们把一个观测视为一个多维向量，维数由变量数决定）。
5. ward 法：也一个类由质心代表，但它将两个类合并时所导致的 SSE  的增加来度量两个类之间的距离。

这里插一句嘴，为什么层次聚类更适合小样本呢？就是因为，观测每多一个，在计算类之间距离的时候，次数就要多一倍，这个计算的复杂性是成阶乘上涨的，所以它一般用于小样本。但是，前人也研究出了一些聚类分析的可伸缩方法，这个是后话。

2.2. R 语言实现

d <- dist(x, method=)

# 选定点与点之间计算距离的方式并生成距离矩阵

fit <- hclust(d, method=)

# d 为之前生成的距离矩阵，method 为类与类之间的距离定义方式

plot(fit, hang=-1)

# 画出树状图

library(NbClust)

devAskNewPage(ask=TRUE)

nc <- NbClust(x, distance=, method= )

table(nc$Best.n[1,])

# 用于选择聚类的个数，看哪种聚类个数得到更多评判准则的赞同

clusters <- cutree(fit, k=5)

table(clusters)

# 展示 5 类聚类方案中每一类有多少观测

aggregate(x, by=list(cluster= clusters),median)

# 描述聚类

# x 为用于聚类的数据，或者为标准化之后的数据

plot(fit, hang=-1)

rect,hclust(fit, k=5)

# 画出树状图，并叠加5类方案

3. 避免不存在的类

利用 NbClust 包中的立方聚类规则可以帮助我们揭示不存在的结构。

plot(nc$All.index[,4], type="o", ylab="CCC")

# nc为 NbClust() 函数计算的到的结果

CCC 值为负并且对于两类或多类递减是，就是典型的单峰分布，表明没有类存在。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏1 回帖

关键词：数据分析 聚类分析 R语言 KINGDOM Species R语言 聚类分析

学习学习，谢谢~