伯努利分布与频率分布的比较-经管之家官网！

扫码加入统计交流群

伯努利分布和频率分布是统计学中两种不同的概念，它们在应用和理解上有着显著的区别。

伯努利分布

伯努利分布是一种离散型概率分布，用于描述只有两种可能结果的随机试验。这种试验通常被称为“伯努利试验”，例如抛一次硬币，结果可能是正面（成功）或反面（失败）。伯努利分布的参数为 $p$p，表示成功的概率，失败的概率则为 $1-p$1p。其概率质量函数（PMF）可以表示为：

$P(X = x) = p^x (1-p)^{1-x}$P(X=x)=px(1p)1x

其中 $X$X 是随机变量，取值为 0 或 1，分别对应失败和成功。

概率总结4——伯努利分布、 … blog.csdn.net

伯努利分布的期望值和方差分别为：

$E(X) = p$E(X)=p

$\text{Var}(X) = p(1-p)$Var(X)=p(1p)

伯努利分布是二项分布的特例，当试验次数 $n = 1$n=1 时，二项分布退化为伯努利分布。

频率分布

频率分布是指在一系列观测数据中，各个观测值出现的次数（频率）的分布。频率是观察到的事件在总观测次数中的比例。随着样本数量的增加，频率会逐渐接近理论概率。

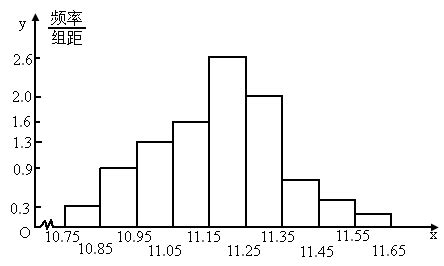
累计频率分布图怎么画,累计图怎么画,累计次数分布图怎么画_大山谷图库

在统计学中，频率通常用于估计概率。例如，在多次抛硬币的实验中，正面出现的频率可以用来估计正面出现的概率。当样本量足够大时，频率会趋近于理论概率。

比较

1. 定义和应用场景：

   • 伯努利分布：适用于描述单次伯努利试验的结果，如抛硬币、投骰子等。
   • 频率分布：用于描述多次试验中某一事件出现的频率，适用于更广泛的统计分析场景。

2. 参数和计算：

   • 伯努利分布：参数为 $p$p，表示成功的概率。
   • 频率分布：参数为频率，即观测值出现的次数与总观测次数的比值。

3. 期望和方差：

   • 伯努利分布：期望 $E(X) = p$E(X)=p，方差 $\text{Var}(X) = p(1-p)$Var(X)=p(1p)。
   • 频率分布：期望值等于理论概率，方差取决于样本量和概率。

4. 关系：

   • 频率分布可以视为对伯努利分布的估计，尤其是在多次试验的情况下，频率逐渐接近理论概率。

结论

伯努利分布和频率分布在统计学中各有其独特的应用领域。伯努利分布主要用于描述单次试验的结果及其概率特性，而频率分布则用于描述多次试验中事件出现的频率及其变化趋势。理解这两种分布的区别和联系，有助于更好地进行数据分析和概率计算。

「经管之家」APP：经管人学习、答疑、交友，就上经管之家！
免流量费下载资料----在经管之家app可以下载论坛上的所有资源，并且不额外收取下载高峰期的论坛币。
涵盖所有经管领域的优秀内容----覆盖经济、管理、金融投资、计量统计、数据分析、国贸、财会等专业的学习宝库，各类资料应有尽有。
来自五湖四海的经管达人----已经有上千万的经管人来到这里，你可以找到任何学科方向、有共同话题的朋友。
经管之家（原人大经济论坛），跨越高校的围墙，带你走进经管知识的新世界。
扫描下方二维码下载并注册APP