古时候的人较量高下,喜欢摆阵让他人来破,本人今天也向古人学习一下。 本人在此摆阵,诚邀各路经济学高人来破我这个小阵。不过,对于不认同边际效用递减规律、经济人追求利益最大化规律和任何物品的效用大小只有经济人自己知道这三个基本前提规律的朋友,就不要来参与了,因为我们的问题焦点都不在一起,或许你会对无差异曲线都不认同,那自然没法讨论了。
我这一阵的论点是:希克斯和斯卢茨基在低档物品的收入效应的分析理论中,所采用的两条无差异曲线根本就不是同族无差异曲线,所以他们在这个方面上的理论是错误的!
第一种证明方法:
下面这个图应该是大家都见过的,不过为了分析,我们过I点竖直向上引一根直线与无差异曲线L2相交,设交点为M(X1’’,X2’’’’),如下图所示:
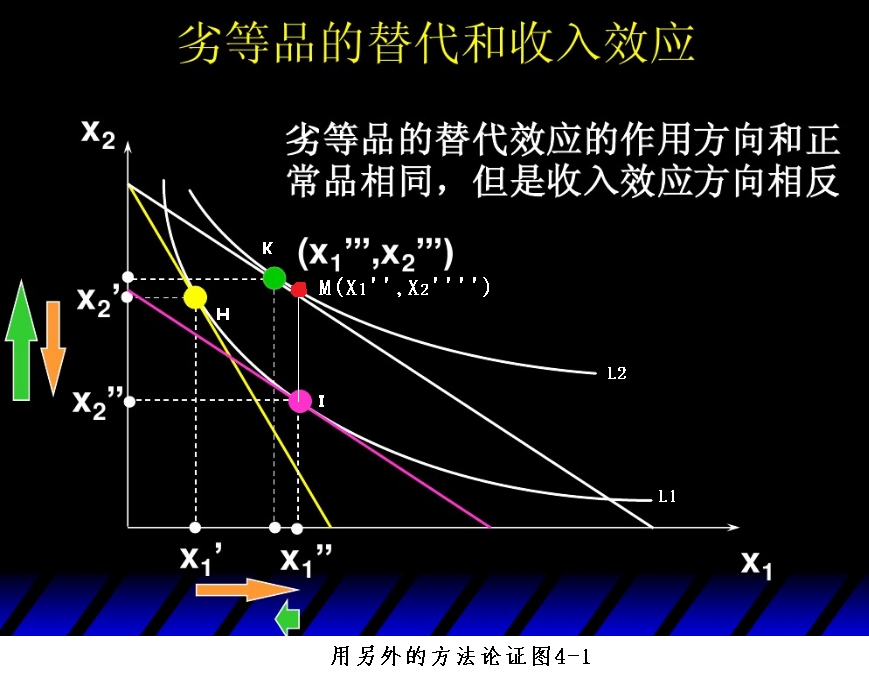
从上图中可以看出,无差异曲线L1在I点的切线比无差异曲线L2在M点的切线更加陡峭,所以X1物品在I点的边际替代率大于M点的边际替代率。
现在我们需要好好思考一个问题了:如果在横轴上的X1’’处减少一个微小量ΔX1,为了抵消减少微小量ΔX1所减少的效用,两条无差异曲线L1和L2上面的I点和M点都需要向左移动一个微小量,以使X2物品的数量增加,来抵消减少微小量ΔX1所减少的效用,那么I点需要增加的X2物品更多还是M点需要增加的X2物品更多呢?
根据边际效用递减规律可以知道,因为X2物品在X2’’处每一单位的边际效用大于X2’’’’处的边际效用,所以抵消减少微小量ΔX1所减少的效用,I点需要增加的数量必定小于M点需要增加的数量。所以X1物品在I点的边际替代率必定小于M点的边际替代率。
现在问题出来了。根据上图的分析可以得出结论:X1物品在I点的边际替代率大于M点的边际替代率。而根据边际效用递减规律又可以得出结论:X1物品在I点的边际替代率必定小于M点的边际替代率。这两个结论完全相反,那么到底是上面那个图错误了,还是边际效用递减规律错误了呢?
无差异曲线理论体系本身就是依据边际效用递减规律所推导出来的,所以我相信在这个问题上没有人会否定边际效用递减规律,那么唯一的可能就是上图中的无差异曲线L2根本就不是无差异曲线L1的同族无差异曲线。
如果是这样的话,那么新的问题又出现了——斯卢茨基和希克斯对低档物品的收入效用理论又怎么能够成立呢?
第二种证明方法分三步:第一步,先用总效用曲线推导出无差异曲线;第二步,在第一步的基础上分析同族无差异曲线之间隐性存在的关系特征规律;第三步,直接引用大家常用的低档物品的收入效应分析图进行分析。
下面在下开始论证:
第一步
用总效用曲线推导无差异曲线
经济人的行为是需要动机的,驱使经济人支持还是反对交易的根本动机——是利益。对于交易行为来说,如果他认为交换所得之物的效用大于他所失去之物的效用,那么这个交易就为他带来了好处,他自然会支持进行交换;如果他认为交换所得之物的效用等于他所失去之物的效用,那么这个交换就不能为他带来任何好处和坏处,他将认为这个交换是完全没有意义的事;如果他认为交换所得之物的效用小于他所失去之物的效用,那么这个交换将为他带来坏处,他必然会反对进行交换。
经济人具有趋利特征,所以要研究一个经济人的交易行为,或许只能从交易使经济人获得利益的多少来进行分析,因为这是人们进行交易的根本动机。如果我们能够知道参与交易的两种物品分别对于该经济人的效用关系,那么我们就可以知道交易使得经济人获得利益的多少关系。
我们假设a财货和b财货不是同一类型的财货,也不能满足同一类欲望。经济人A拥有m个a财货,他打算同拥有n个b财货的经济人B进行交易,一般来说经济人A可能会盘算出多种交换比例和交换数量。现在假设经济人A认为a、b两种物品对于他的效用关系分别如图2-1中两条总效用曲线所示,那么使得经济人A支持、反对和认为是无意义的交换方案分别是那些呢?

我们可以将上面第一个图以Qa为旋转轴,翻转一下。将第二个图以原点为旋转点,向左旋转90°。然后将新得到的两个图的原点重合,并添加一跟与TUa轴和TUb轴都是45°的辅助直线段,那么可以得到下面这样一个图:

这个图是由四个平面合并而成,包括一个物品数量组合平面、一个效用组合平面和两个数量-效用关系平面,所以我们将这个图称之为四合图。我先将上面这个四合图中所涉及到的和所反映出的几个方面说明一下,这样更加有利于大家理解这个图:
1、四合图直角坐标系中每一个轴都是正数轴,没有负数轴,这一点与我们通常使用的直角坐标系是不同的;
2、所添加的辅助直线段与TUa轴和TUb轴都是45°的,它其实就是一根等效用线,在这根辅助直线段上面的每一个点的总效用都相等(坐标值相加都相等)。该线距离原点的垂线距离越远,那么总效用就越大,反之就越小。为了更加方便,我们将这根辅助直线段称之为等效用线段。
3、等效用线段上面的任意一点x的坐标(TUb1,TUa1),必然对应持有组合y点的坐标(a1,b1)。因为a1数量的a物品的效用是TUa1,b1数量的b物品的效用是TUb1。
4、如果我们将x、a、b视为可以在各自曲线上移动的活动点,那么在等效用线段上面移动x点,b、a、y三点也必将移动。Y点运动的轨迹将是一个左高右低、凸向原点的曲线,它就是我们所知道的无差异曲线。如同图中的红色线所示。
5、经济人A拥有m个a物品,所对应的效用点恰恰是等效用线段的下端点,所以点(m,0)必然也是图中这条红色无差异曲线上面的一点。
6、如果等效用线段平行靠近原点,总效用就会减少,那么y点的轨迹所形成的无差异曲线必定也会靠近原点;反之,如果等效用线段平行远离原点,总效用就会增大,那么y点的轨迹所形成的无差异曲线必定也会远离原点。所以斜向拖动等效用线段就能够得到a和b物品对于经济人A的所有无差异曲线,即一族无差异曲线。
7、无差异曲线上每一点的斜率与该点所对应的两条总效用曲线上两点的斜率具有严格的数学关系。如果分别设y点、a点、b点在各自曲线上的斜率为Ky、Ka、Kb,(四合图中各个平面不区分正负方向,所以斜率一律为正值)那么,无差异曲线上每一点的斜率Ky等于该点在水平和竖直方向上所对应的两条总效用曲线上a点和b点的斜率Ka和Kb的乘积,即:Ky=Ka×Kb。
8、从数学意义上看,边际效用Mu是总效用TU曲线的斜率。四合图中b物品的总效用曲线是以原点为旋转点,向左旋转90°而得到,所以在四合图中b物品的总效用曲线的斜率等于b物品边际效用的倒数,即Kb等于1/MUb;a物品的总效用曲线是以水平轴翻转而得到,所以在四合图中斜率不变(如果要计算正负的话,那么翻转后就斜率就为负,但我们的分析中不计算正负),Ka等于MUa。由前面的等式Ky=Ka×Kb可知,无差异曲线上每一点的斜率Ky等于该点在水平和竖直方向上所对应的两条总效用曲线上a点的边际效用MUa除以b点的边际效用MUb,即:Ky=MUa/MUb。
综上所述,我们可以得出如下结论:
1、所有使经济人A持有两种物品的组合在红色无差异曲线下部的交换方案,他都会反对,因为这些交换方案的结果给他带来了坏处。
2、所有使经济人A持有两种物品的组合恰好落在红色无差异曲线上的交换方案,他都会认为完全没有意义,因为这些交换方案的结果对于他来说,既没有好处也没有坏处。
3、所有使经济人A持有两种物品的组合在红色无差异曲线上部的交换方案,他都会赞成,因为这些交换方案的结果给他带来了好处。
4、m点所在的无差异曲线,划分出了经济人A在有m数量的a物品时的所有得到和付出之间的大于和小于关系的边界,所以我们可以将这条无差异曲线称之为经济人A的交易边界曲线。从图中就直接可以看出:经济人A的交易边界曲线具有单调递减性。该边界曲线上的每一点都分别表达了经济人A的得到和付出的边界关系,例如曲线上的y点就表达了两种边界关系:一、经济人A得到b1数量的b物品,他最大愿意付出的代价为m-a1数量的a物品;二、经济人A付出m-a1数量的a物品,他希望至少得到b1数量的b物品。
现在我们已经知道,可以用总效用曲线在四合图中推导出经济人A对两种财物的不同组合的无差异曲线。不过有一点值得特别说明:在论证中用到了一个假设“a财货和b财货不是同一类型的财货,也不能满足同一类欲望”。同类型的财物往往满足的是同一类的欲望,那么其中任何一种财物对于经济人的边际效用发生变动时,将使另一种财物对于该经济人的边际效用也会发生变化,所以自然就不能用我们刚才的方法来推导无差异曲线。比如说:用货币交换货币、用苹果换苹果、用一种冰激凌交换另一种冰激凌等等情况,都会存在这样的问题。不过所幸的是在一般的经济生活中,大家都是用货币与其它财物进行交易,所以出现这种例外的情况很少且不重要,对此不必再多费笔墨。且在这一个问题方面,我们现在的技术还不能提供什么新的方法进行解决。在我们后面的所有论述中,都隐含的存在这种避让,请各位读者注意这个问题。






 雷达卡
雷达卡










 京公网安备 11010802022788号
京公网安备 11010802022788号







